Is a superflare capable of changing a planets orbit?

[Edward Barrow]

I'm examining if a massive superflare early in the solar systems history could be the explanation for the odd positions of certain planets and moons in our solar system (and their rotations). For this test, I've taken Mars as an example.

I’m going to place Mars in the early solar system in an orbit 80m Km from the sun and see if a superflare could blast it out to its current orbit in the solar system at 228m Km from the sun. For aesthetic purposes, here is a diagram of the famous XZ Tauri superflare superimposed (to scale) on our solar system:

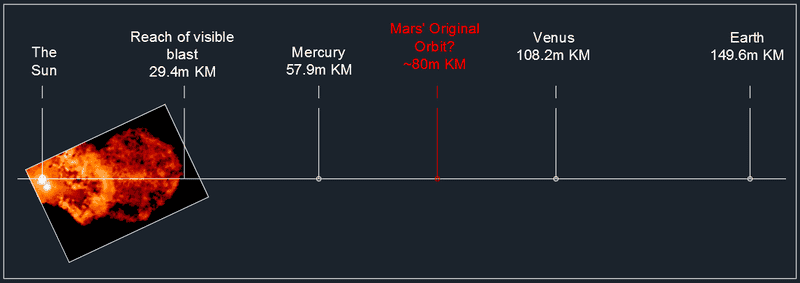
I’m going to do some very simplified calculations.

Mass of Mars = 6.42 * 1023 kg. Mass of the Sun = 1.99 * 1030 kg. The kinetic energy of an orbiting body is KE = G(M*m/2r) where G is the gravitational constant, M is the mass of the body being orbited, m is the mass of the orbiting body, and r is the semi-major axis.

Taking the proposed initial distance from the Sun of Mars as halfway between where Mercury and Venus currently are, so r = 8.31 * 1010meters. At this initial distance (I’m omitting writing units for the sake of clarity, but I have set everything to SI units) KE = (6.67 * 10-11)(1.99 * 1030 * 6.42 * 1023) / (2 * 8.31 *1010) = 5.13 * 1032 Joules. The current semi-major axis of Mars is r = 2.28 * 1011 meters. Solving for the current orbital kinetic energy, KE = (6.67 * 10-11)(1.99 * 1030 * 6.42 * 1023) / (2 * 2.28 * 1011) = 1.87 * 1032 Joules. The difference between these energies (simply 5.13 * 1032J – 1.87 * 1032J) is 3.26 * 1032Joules. So Mars would need 3.26 * 1032Joules of energy to move from its proposed initial orbit to its current orbit.

Looking at https://en.wikipedia.org/wiki/Superflare (I couldn’t find a better source that listed superflare energies with actual numbers) I converted the highest energy superflare 2 * 1038 erg to 2 * 1031 Joules. This is the highest energy superflare they have listed (and it’s even a G type star like our Sun.) 2 * 1031 Joules is an order of magnitude away from the 3.26 * 1032 Joules needed to move Mars. For the sake of comparison, our Sun’s solar flares typically release around 1 * 1020 Joules of energy, the greatest of them releases 1 * 1025 Joules, and a million times the biggest events is only 1 * 1031Joules. Additionally, I did not even calculate the gravitational potential energy of Mars which would also have to be accounted for if we are moving from one orbit to another. Based on these calculations, I do not think a solar superflare would produce enough energy to move Mars.

I guess an additional consideration with an event like this is the infinitesimal surface area of Mars compared to the fact that a superflare could be emitted in any direction, its energy spreads and decreases per square meter as it moves through space, and even an absolutely direct hit would only impart of fraction of the total energy of the superflare.

So, is the proposal dead in the water? Superflares simply cannot move planets? Or am I missing something? I don't know if pressure radiation or gravitational waves could play a role. These are outside my area of expertise.

 

[stefan r]

How much mass is in the flare? How much of the planet mass is matter accreted from flares?

edit, also you have the energy of Mars orbit lower than the hypothetical orbit between Venus and Mercury. That cannot be right because something higher in a gravity well has more energy. You need to add the potential energy. The energy Mars would gain falling from its current position to the lower orbit.

 

[Edward Barrow]

you have the energy of Mars orbit lower than the hypothetical orbit between Venus and Mercury. That cannot be right because something higher in a gravity well has more energy. You need to add the potential energy. The energy Mars would gain falling from its current position to the lower orbit.

So I've underestimated the amount of energy Mars has in its current orbit? This sounds like it makes the idea of a superflare altering the orbit of a planet even more unlikely. I guess interactions with other planetary bodies after a superflare could change things up a bit (like a close fly by with another planet, I've drawn in Earth as an example) but that might be grasping at straws:

This picture is of course exaggerated. It would take many many rotations around the sun for a planet like Mars to go from an original orbit to its current orbit.

 

[rootone]

It's plausible, but no more plausible than gravitational interaction with a relatively small solar system passing nearby, which is now not visible

 

[stefan r]

It's plausible, but no more plausible than gravitational interaction with a relatively small solar system passing nearby, which is now not visible

Gravitational Interaction would effect many planets. It is possible, but highly unlikely that the interaction would be in the ecliptic plane.

So I've underestimated the amount of energy Mars has in its current orbit? This sounds like it makes the idea of a superflare altering the orbit of a planet even more unlikely. I guess interactions with other planetary bodies after a superflare could change things up a bit (like a close fly by with another planet, I've drawn in Earth as an example) but that might be grasping at straws:
. It would take many many rotations around the sun for a planet like Mars to go from an original orbit to its current orbit.

The event time has to be before the late-heavy bombardment period. http://www.space.com/16153-mars-impact-crater-map.html
Picture someone playing volley ball. The sphere deforms when the hand impacts the ball. A centimeter deformation of a volley ball is many kilometers on Mars size sphere. May be more like an egg instead of a volleyball. The surface could liquefy. Certainly Mars quakes. Also a lot of the energy you are bringing from the flare is radiation and thermal. The surface rock would be vapor then raining liquid glass. Evidence of asteroid impacts from before the event would be erased.

I'm wondering about the superflare energy. They claim 10^32 joules. If the mass in the flare is around planetary mass then it might not have outward momentum. Suppose the energy did work lifting the mass up to mercury. You now have stationary plasma. If mercury runs into the plasma it would slow down mercury a little and lower the orbit.
total energy minus work lifting mass up sun's gravity well minus thermal energy gives the kinetic energy of the flare when it reaches the orbit.

 

[Janus]

So I've underestimated the amount of energy Mars has in its current orbit?

No, you just forgot the minus sign. Total orbital energy is the sum of kinetic and gravitational potential energy. Gravitational potential energy is expressed as:
$$- \frac{GMm}{r}$$ and thus becomes less negative or greater as r increases.

The sum can be expressed as
$$E = \frac {mv^2}{2}- \frac{GMm}{r}$$
with v being the orbital velocity.

For a circular orbit,
$$v= \sqrt{\frac{GM}{r}}$$

If we substitute this for v we get
$$E=-\frac{GMm}{2r}$$

and for elliptical orbits you can use the semi-major axis for r.

 

[Bandersnatch]

Now that you have proper value for the mechanical energy of the two orbits calculated, you need to consider three more things.
One is the proportion of total energy emitted by a flare that hits the planet. I don't know how focused flares are, but they are certainly not laser beams - in the worst case, the energy will spread with the inverse square of the distance from the star. This will net you only a fraction of the listed flare energy that could affect the planet.
Second is what fraction of the energy hitting the planet would be converted into orbital energy, and not e.g. re-emitted or reflected. This will further reduce the available energy.
Third is orbital mechanics - a flare is a one-off event that can impart only a one-off impulse to the orbiting body. What this means, is that the outward spiral as depicted is not a possible result of being hit by a flare. An orbiting body that does not have a constant force acting on it will always follow an orbit that is a conic section. Here, it means an ellipse of one eccentricity or another. After being hit by the flare, the orbit would become more eccentric, the distances of closest and farthest approach to the star would change, but it'd still be an ellipse that must include the point where the planet was originally and the star as one of the foci.
Below is an example of an orbital change from one ellipsis to another after a single burn directed partially outwards. This is the sort of thing you should expect.

(image credit: Mark Adler)

 

[nikkkom]

A significant fraction of flare energy is in EM radiation (light, X-rays and such). This energy will be very inefficient in altering planet's orbit - it is not focused (radiates over the entire half of the sky visible from flare location).

 

[Edward Barrow]

I've created a new version of my previous image. I've colored Mars' original orbit in blue to match Bandersnatches diagram, and the path it takes after being blasted outwards in orange.

As you can see, if Mars gets too close to Earth, Earth will gravitationally pull Mars towards the Earth altering Mars' orbit again. This could potentially swing Mars around the Earth and out into its new orbit at 228m Km from the sun. I'm not sure what would happen to the Earth though. Would it fall in closer to the sun or be pulled outwards too?

 

[stefan r]

... close to Earth, Earth will gravitationally pull Mars towards the Earth altering Mars' orbit again. This could potentially swing Mars around the Earth and out into its new orbit at 228m Km from the sun. I'm not sure what would happen to the Earth though. Would it fall in closer to the sun or be pulled outwards too?

Yes. Any two orbiting bodies will trade momentum. As you drew it the "earth" would be pulled into a lower orbit. You could have an alternate case where Mars flies in front of Earth and gets pulled back slightly. In the alternate case the event needs much more energy.

We know little about super-flares. I have an oxy-acetlyene torch. It might help to consider trying to move a car with a torch. I do not believe my torch at full power will budge my economy car even when in neutral. I have not tested. The when cutting with oxy-acetlyene some slag can fly up to a meter away. I generally do not clamp a piece that I am cutting. If we assemble a HUGE torch or maybe borrowed a space shuttle engine from NASA we could probably get enough motion in the car to call it "accelerated". The remains would not be in the same place where I left the car. However, the remains would not resemble my car. The license plate, registration, and VIN number would no longer be readable.

 

[Edward Barrow]

We know little about super-flares. I have an oxy-acetlyene torch. It might help to consider trying to move a car with a torch. I do not believe my torch at full power will budge my economy car even when in neutral. I have not tested. The when cutting with oxy-acetlyene some slag can fly up to a meter away. I generally do not clamp a piece that I am cutting. If we assemble a HUGE torch or maybe borrowed a space shuttle engine from NASA we could probably get enough motion in the car to call it "accelerated". The remains would not be in the same place where I left the car. However, the remains would not resemble my car. The license plate, registration, and VIN number would no longer be readable.

I agree with you. I don't think the actual superflare itself is capable of moving anything without destroying it in the process. I'm just wondering if some other secondary force (as a result of the superflare) could move bodies in the solar system.

Pressure radiation is a possibility.

According to wikipedia (https://en.wikipedia.org/wiki/Radiation_pressure), solar radiation pressure is a source of orbital perturbations. It affects the orbits and trajectories of small bodies and all spacecraft . For example, had the effects of the sun's radiation pressure on the spacecraft of the Viking program been ignored, the spacecraft would have missed Mars orbit by about 15,000 kilometers. The radiation pressure results in forces and torques on the bodies that can change their translational and rotational motions.

I suspect there was a massive blast from the sun in the solar systems history, and this could have had an effect on planets and moons. There is evidence such a blast happened:

Prof. Says Solar Flash Created Glazed Areas on Lunar Surface

A Cornell astronomer has said he believes a giant explosion of the sun in recent geologic times glazed some areas on the moon’s surface and created some of the glassy material reported by the Apollo 11 astronauts.

Prof. Thomas Gold, director of Cornell’s Center for Ftaidophysics and Space Research, said a solar outburst must have occurred not more than 100,000 years ago. The apparently thin coating of glaze, Gold said, indicates the – tremendous solar blast was of short duration — probably between 10 and 100 seconds. Gold’s conclusion, based on photographs taken by Neil A. Armstrong andd Edwin A. Aldrin, was reported today in Science, the weekly publication of the American Association for the advancement of Science.

Glassy patches that can be seen clearly in the photographs. Gold said, range in size from a half millimeter to one centimeter. According to Gold, “Points and edges appear to be strongly favored for the glazing process. In some cases, droplets appear to have run down an inclined surface for a few millimeters and congealed there.”

The time of occurrence of the flash heating, Gold said, would have to have been sufficiently recent for micrometeorites not to have destroyed the glaze, nor for the mechanisms that redistribute the lunar soil to have blanketed the objects. The astronauts, Armstrong and Aldrin, described the locations in which the glassy patches on the surface were found. They said that this was invariably in the middle of little craters in the two to four-foot size range.

Gold said this position indicates that the locations would have been particularly favorable for melting from a source of intense radiation. If the sun was responsible, it must have flared up to 100 times its present intensity. Solar flares are known to occur, but are very much weaker than that. Gold speculated that the phenomenon might be in the nature of a very minor nova-like outburst of the sun. A nova’ is a star which is made several million times brighter by an outburst and then gradually fades back to its original brightness.

“One cannot completely rule out the possibility that stars, like the sun, do have occasional instabilities of internal origin, but very much weaker than the real novae,” Gold said, “and outbursts to only a hundred times the original brightness for a few seconds would hardly have been detected on other stars of the solar class.” The moon was particularly affected by the solar phenomenon, he said, because it has no protective atmosphere. The total heat delivered to the Earth would have been spread throughout the atmosphere and would not have caused a substantial rise in the temperature of the lower atmosphere or of the ground.

(Source: The Cornell Daily Sun, Volume 86, Number 13, 26 September 1969 “Prof. Says Solar Flash Created Glazed Areas on Lunar Surface” )

Maybe if a superflare can't move a planet, a "minor nova-like outburst" might. Though the article does not indicate how strong such an outburst might be, and if it would be more powerful than a superflare.

 

[rootone]

It's certainly not yet explained how Uranus and Venus have the unlikely rotational axis that they do.
Also what we know so far of other solar systems suggests that Jupiter is oddly far away from it's host star.

 

[davenn]

According to wikipedia (https://en.wikipedia.org/wiki/Radiation_pressure), solar radiation pressure is a source of orbital perturbations. It affects the orbits and trajectories of small bodies and all spacecraft . For example, had the effects of the sun's radiation pressure on the spacecraft of the Viking program been ignored, the spacecraft would have missed Mars orbit by about 15,000 kilometers. The radiation pressure results in forces and torques on the bodies that can change their translational and rotational motions.

I couldn't find any reference for that, can you ?

I suspect there was a massive blast from the sun in the solar systems history, and this could have had an effect on planets and moons. There is evidence such a blast happened:

Prof. Says Solar Flash Created Glazed Areas on Lunar Surface

A Cornell astronomer has said he believes a giant explosion of the sun in recent geologic times glazed some areas on the moon’s surface and created some of the glassy material reported by the Apollo 11 astronauts.

not exactly a good reference ... they are his speculations only
I would like to see if his ideas were peer reviewed, otherwise they are just personal thoughts
There are other ways od generating glassy material ... the major way is from impacts, which the Moon has had a long history of

 

[stefan r]

The energy needed to glaze a few millimeters, << energy needed to liquefy a few meters << energy needed to liquefy the continental shelf.

Flash heating tends to make rock explode away. Changes to the momentum of the planet core will be much lower than changes to the momentum of the surface. Escape velocity from Mars is only 5000 meters per second. If a high velocity wind has enough energy/momentum to accelerate a planetary mass 1000 meters per second it will strip the outside surface of the planet. Much of the energy/momentum will go into the spall which will then leave orbit.

Could a cantaloupe be loaded into a Howitzer and fired

Yes

Is it possible that this here normal looking cantaloupe came to this position because it was fired out of a 155mm howitzer.

No. If that cantaloupe was fired out of a howitzer it would not look like a normal cantaloupe. It would be pulp before leaving the barrel. 1000 m/s wind would skin the peal off. Impact on arrival would destroy a cantaloupe at much lower velocity.

However, all cantaloupes do have a lot of water molecules. It is nearly certain that your cantaloupe has molecules that were fired out of a howitzer and then later got adsorbed by roots and then made into the cantaloupe. There are also a few molecules of Julius Caesar 's piss. These molecules are rare. You will not be able taste them. Mars is effected by the sun's light pressure and by the solar wind. A situation where Mars crosses Earth's orbit is highly unlikely. A situation where some of the planetesimals and dust that formed Mars crossed or passed through the planetesimals and dust that formed Earth is more probable.

 

[Vanadium 50]

Also what we know so far of other solar systems suggests that Jupiter is oddly far away from it's host star.

We know nothing of the sort. We know that if we look for stars with large planets in close-in orbits we find stars with large planets in close-in orbits.

We most certainly do not know that our solar system is sufficiently unusual that we have to invoke some extraordinary mechanism to explain it.

 

[rootone]

Right, I guess that very large planets similarly displaced from the host start as Jupiter is could be common,
just that so far our detection methods for those are relatively weak.
I know I did read in some authoritative source (which I don't remember), that there was reason to believe Jupiter has migrated outwards since forming.
This is a link to that hypothesis, but not the one I read originally, source is a reasonable one though not authoritative.
http://www.space.com/28901-wandering-jupiter-oddball-solar-system.html

 

[stefan r]

Right, I guess that very large planets similarly displaced from the host start as Jupiter is could be common,
just that so far our detection methods for those are relatively weak.

Kepler would have been sensitive enough. You need multiple transits to confirm a planet. Kepler collected data 2009 to 2013. It takes Jupiter 10 years to orbit the sun. A single dimming event could be an object in the Kuiper belt.

I couldn't find any reference for that, can you ?

http://www.fxsolver.com/browse/form...by+Reflection+(using+particle+model:+photons)
Second paragraph last sentence.
Is more fun to read about Shkadov thrusters IMO.

 

[nikkkom]

I've created a new version of my previous image. I've colored Mars' original orbit in blue to match Bandersnatches diagram, and the path it takes after being blasted outwards in orange.

View attachment 194602

As you can see, if Mars gets too close to Earth, Earth will gravitationally pull Mars towards the Earth altering Mars' orbit again. This could potentially swing Mars around the Earth and out into its new orbit at 228m Km from the sun.

No, it won't put Mars on "orbit at 228m Km from the sun". Specifically: even if the resulting orbit does reach 228m distance from the Sun, it won't be circular, Mars _must_ continue to repeatedly return to the location where it had an encounter with Earth.

 

[davenn]

.....

http://www.fxsolver.com/browse/formulas/Radiation+Pressure+by+Reflection+(using+particle+model:+photons)
Second paragraph last sentence.
Is more fun to read about Shkadov thrusters IMO.

ahhhhh, that's better :)