laser
- 104
- 17
- Homework Statement
- See image in description
- Relevant Equations
- V=iR
Image from Wiley Intro Physics Textbook sample problem
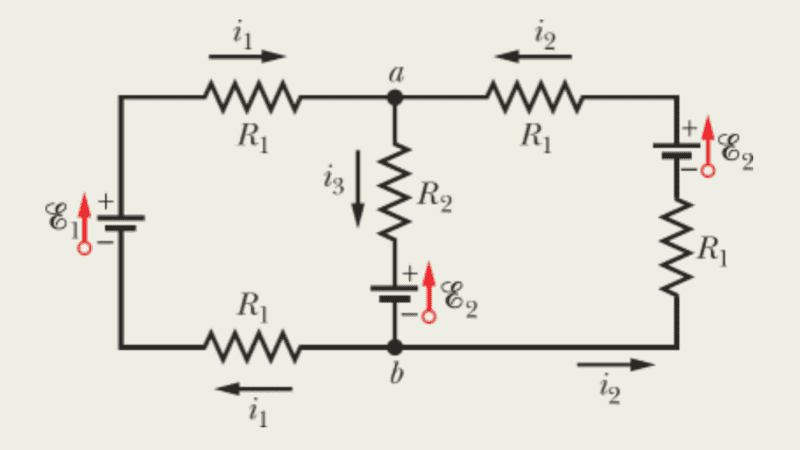
This was the given problem. In the diagram, one can see that the current flowing into each battery equals the current flowing out of each battery. Is this always the case, and why?
If there was only one battery, I guess it could be considered conservation of charge, but for eg the battery on the left, why can't 2A flow out and 1A flow in?
This was the given problem. In the diagram, one can see that the current flowing into each battery equals the current flowing out of each battery. Is this always the case, and why?
If there was only one battery, I guess it could be considered conservation of charge, but for eg the battery on the left, why can't 2A flow out and 1A flow in?