MatinSAR
- 673
- 204
- Homework Statement
- Find the electric flux passing through surface 1 and surface 2.
- Relevant Equations
- Gauss's Law
Picture :
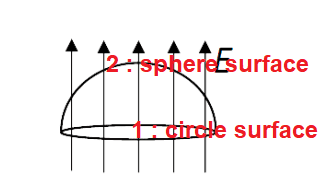
My answer :
I guess net electric flux is 0.
so electric flux passing through surface 1 = -(electric flux passing through surface 2)
and electric flux passing through surface 1 is EA = E(pi)(r^2)
Is it correct? Thank you ...
My answer :
I guess net electric flux is 0.
so electric flux passing through surface 1 = -(electric flux passing through surface 2)
and electric flux passing through surface 1 is EA = E(pi)(r^2)
Is it correct? Thank you ...