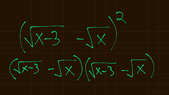mathdad
- 1,280
- 0
The picture shows a simple problem. However, my question has to do with multiplication of radicals.
I know how to use FOIL.
sqrt{x - 3} • sqrt{x} is slightly confusing.
Do I multiply radicand times radicand?
My question is:
Does sqrt{x - 3} • sqrt{x} become sqrt{x^2 - 3x} in the FOIL process?
View attachment 7895
I know how to use FOIL.
sqrt{x - 3} • sqrt{x} is slightly confusing.
Do I multiply radicand times radicand?
My question is:
Does sqrt{x - 3} • sqrt{x} become sqrt{x^2 - 3x} in the FOIL process?
View attachment 7895