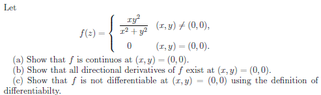Is It Enough to Show Continuity and Directional Derivatives?

[GreenGoblin]

View attachment 639I am attaching a pico of the question as I don't think of how I can adequately write this up with text and symbols. Ok, so, I have one problem in my find. I know that it is continuous, if the limit as it approaches the point (in this case (0,0) = the function evaluated at that point). BUT, we already have that it is defined as 0 at this point. and the limit of 0 is 0 so this is trivially true.. but more is expected to be written here.. its not enough marks for this. Is this ok what I am doing? do i have to show that xy^2/x^2+y^2 goes to 0? or that 0 goes to 0 :s. part 2 what is meant by 'directional' differatives? is it partial differatives? just as normal i find dz/dx, dz/dy? and second orders too or not? i think the question isn't clear what is expected to calculate.

 

[jakncoke1]

You have to show that Any sequence $X_n \in \mathbb{R} \times \mathbb{R}$ s.t that $X_n \to (0,0)$, $f(X_n) \to L$ and L = 0.

As for directional derivatives, you have to show that $lim_{h \to 0} \frac{f(x+hv)-f(x)}{h}$ exists along any 2 dimensional vector v at point (0,0) = x

so $\displaystyle \lim_{h \to 0} \frac{f(hv)}{h}$ has a limit for a non zero vector v.

 

[GreenGoblin]

huh?i posted a pica.of the problem. that can't be the answer because this is not x, this is (x,y) so the answer has to be as much to do with y as x.

 

[jakncoke1]

huh?i posted a pica. of the problem. that can't be the answer because this is not x, this is (x,y) so the answer has to be as much to do with y as x.

i used x in the sense that $x \in \mathbb{R} \times \mathbb{R}$, so x = ($x_1,x_2$)

 

[HallsofIvy]

The "difficult" part of showing continuity is showing that the limit is 0. You cannot, for example, just note that if x= 0 the fraction is 0 for any y and so approaching (0, 0) along the y-axis, the limit is 0. You have to show that if you are "close" to (0, 0), in any direction, the value of the function is "close" to 0. I think the simplest way to handle this is to change to polar coordinates. That way, the single variable, r, measures the distance from (0, 0). $$x= r cos(\theta)$$, $$y= r sin(\theta)$$, and $$x^2+ y^2= r^2$$ so this fraction becomes
$$\frac{r^3cos(\theta)sin^2(\theta)}{r^2}= r cos(\theta)sin^2(\theta)$$ which clearly is close to 0 for r close to 0.

No, "directional derivatives" are not, strictly speaking, "partial derivatives". The "directional derivative" is the rate of change as you move in the given direction, not necessarily just in the direction of the x and y axis. The directional derivative of f(x,y) in the direction of unit vector, v, is $$\nabla f\cdot v$$. Equivalently, the directional derivative of f(x, y) in direction $$\theta$$ to the positive x-axis is $$cos(\theta)\frac{\partial f}{\partial x}+ sin(\theta)\frac{\partial f}{\partial y}$$. To determine whether or not the directional derivatives exist at (0, 0), replace y with mx and take the ordinary derivative of the resulting function of x. That works for all "directions" except along the y-axis where, of course, the directional derivative is just the partial derivative with respect to y.

As for showing that the function is not "differentiable" at (0, 0), what definition of "differentiable" are you using for a function of two variables?

(Note that the function, f(x,y), defined to be 0 if xy= 0, 1 if xy is not 0, has both partial derivatives at (0, 0) but is not even continuous there.)

 

[GreenGoblin]

right but the function is defined as 0 at (0,0). so it has to be continuous as lim 0 = 0, and f(0,0) = 0 ?? :s I am stuck because it seems trivially true.

 

[jakncoke1]

Take the following function$$f(x,y) = \left\{
\begin{array}{lr}
(x+y+1,\frac{x^2-y^2}{x^2+y^2}) & : (x,y) \not = (0,0)\\
(1,0) & : (x,y) = (0,0)
\end{array}
\right.
$$

Then f(0,0) = (1,0)
But Take the sequence $X_j$ = ($\frac{1}{j}$,0) where $j \in \mathbb{N}$
then $X_j \to (0, 0)$ as $j \to \infty$

but $lim_{j \to \infty}f(0,\frac{1}{j}) = (\frac{1}{j} + 1, 1) \to (1,1)$
but (1,1) $\not = f(0,0) = (1,0)$.

 

[GreenGoblin]

Take the following function$$f(x,y) = \left\{
\begin{array}{lr}
(x+y+1,\frac{x^2-y^2}{x^2+y^2}) & : (x,y) \not = (0,0)\\
(1,0) & : (x,y) = (0,0)
\end{array}
\right.
$$

Then f(0,0) = (1,0)
But Take the sequence $X_j$ = ($\frac{1}{j}$,0) where $j \in \mathbb{N}$
then $X_j \to (0, 0)$ as $j \to \infty$

but $lim_{j \to \infty}f(0,\frac{1}{j}) = (\frac{1}{j} + 1, 1) \to (1,1)$
but (1,1) $\not = f(0,0) = (1,0)$.

what has that got to do with anything? i already don't like you.

 

[Jameson]

what has that got to do with anything? i already don't like you.

Those were the magic words. Thread closed.