Is it maximum voltage or RMS voltage

[jaus tail]

Homework Statement

Homework Equations

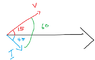
I drew phasors and got the answer. Angle between V and I is 60 degrees. Cosine of 60 is 0.5. Then I multiplied V and I and divided it by 2.

The Attempt at a Solution

I got answer 62.5. But I'm not sure if values of V and I given are rms values or maximum value.
Isn't formula for Power as: Vrms * I rms cos(angle)
So shouldn't it be: 25/1.414 * 5/1.414 * cos(angle)?

 

[Baarken]

The book that I have (Power System Analysis by Charles A. Gross) write phasors using the rms value, i.e. the phasor $V= \frac{V_{max}}{\sqrt{2}} \angle \phi$

 

[K Murty]

Hi.
It is a convention to express the value of the voltage or current phasor as the RMS magnitude of it. Much like the passive sign convention, this is widely known and acknowledged in electronics, unless stated otherwise.

That is, if:
$$V_{m} \cos ( \omega t + \alpha) = \Re({V_{m} \cdot e^{j( \omega t + \alpha) } }) = \Re( {V_{m} \cdot e^{j (\omega t) } \cdot e^{j (\alpha )} } ) \underbrace{ \rightarrow }_{\text{Phasor domain/ transform} } \frac{ V_{m} }{ \sqrt{ 2 } } \angle{\alpha}$$
The above is, of course, if you are using the cosine definition of a phasor, you can also use a sine definition in which case the signal would have to be phase shifted to the right by 90 (add - 90 ) to your cosine. The relation between peak and RMS for sinusoids is a result of the evaluation of the integral and using the definition of an RMS signal, the proof can be found online but the main concept is that the RMS value allows comparision with DC signals, as far as resistive elements are concerned.

Formula for average power in the AC domain is:
$$\frac{1}{2} \cdot V_{m} I_{m} \cos { ( \alpha_{v} - \alpha_{i} } )$$
Where:
$$V_{m} I_{m}$$
Refer to peak values.
When using RMS, V and I become respective values and the equation is :
$$V_{rms} I_{rms} \cos { ( \alpha_{v} - \alpha_{i} } )$$
Your answer is correct as far as I know.
If you use peak values, you multiply by a half, and if you use rms, you get the same answer as the square root of two is present in both I and V rms.
Thanks for reading.
KM

 

[Babadag]

In my opinion, the voltage and current are rms.

However, when you calculate the apparent power you have to use the conjugate current.

 

[jaus tail]

Okay. So if values are given in form V angle (45^o) then V is the RMS value.
But if it's given like V sin (wt + 45) then V is maximum value. Right?

 

[Babadag]

The result it is S[apparent power-VA]=P[active power-W]62.5+jQ[reactive power-VAR]108.25
In order to achieve this you have to multiply Vے α=V.cos(α),V.sin(α) by Iے β conjugate = Iے -β
I.cos(β),-I.sin(β).

 

[jaus tail]

I'm not sure.
From what I know:
draw V
draw I
and P is V times I times cosine of angle between them
Q is V times I times sine of angle between them
V = 25 angle 15
I = 5 angle -45
So this is

So P is V times I times cos 60... no sin term
Q is V times I times sin 60

I didnt understand this:
Vے α=V.cos(α),V.sin(α) by Iے β conjugate = Iے -β
I.cos(β),-I.sin(β).

 

[Babadag]

Since ,conventional, inductive reactive power has to be positive [and capacitive negative], if the current lags 15+45=60 degrees[ then the angle it is -60 degrees] then:
P=V.I.cos(+60) Q=V.I.sin(+60)
See –for instance:
https://en.wikipedia.org/wiki/Complex_conjugate

 

[jaus tail]

That phasor clears up the I* part. I never understood what its purpose was. Thanks.