- 1,191
- 683
- TL;DR Summary
- Trying to find an expression for cos(40 degrees) (using any combination of radicals)
What sort of number is cos(40) ? You can solve the equation:
$$ 4 \cos^{3}40 -3\cos40+0,5=0 $$
but you end up with complex numbers requiring a cube root. The polar angle gets divided by 3 and you end up needing cos(20) or cos(10) in your answer. No way (it seems) to express as a radical or combination of radicals in any form .
The solution from WA is interesting. There are 3 solutions - as a 'bonus' for solving for cos(40), you also get answers for cos(20) and cos(80).
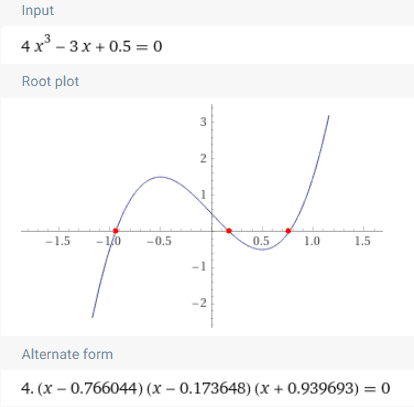
$$ 4 \cos^{3}40 -3\cos40+0,5=0 $$
but you end up with complex numbers requiring a cube root. The polar angle gets divided by 3 and you end up needing cos(20) or cos(10) in your answer. No way (it seems) to express as a radical or combination of radicals in any form .
The solution from WA is interesting. There are 3 solutions - as a 'bonus' for solving for cos(40), you also get answers for cos(20) and cos(80).