kodama
- 1,075
- 144
- TL;DR Summary
- bulk theories of quantum gravity are dual to each other
this paper
arXiv:2310.02958 [pdf, other]
What if Quantum Gravity is "just'' Quantum Information Theory?
Aron C. Wall
Comments: 6 pages, 2 figures. Additional references added to arxiv version
Journal-ref: Proc. 28th Solvay Conf. Phys., ed. D. Gross, A. Sevrin, P. Zoller, World Scientific Publishing Co., Singapore, 2023
Subjects: General Relativity and Quantum Cosmology (gr-qc); High Energy Physics - Theory (hep-th)
except
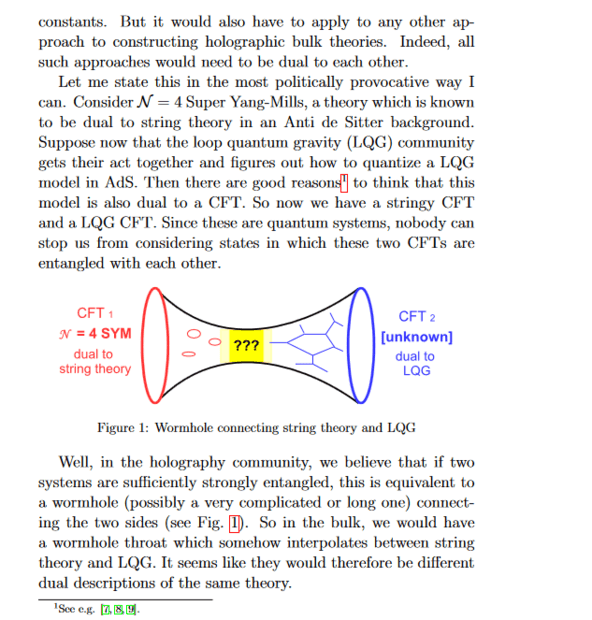 would quantize a LQG model in AdS. via holographybe dual to N = 4 Super Yang-Mills and also string theory
would quantize a LQG model in AdS. via holographybe dual to N = 4 Super Yang-Mills and also string theory
arXiv:2310.02958 [pdf, other]
What if Quantum Gravity is "just'' Quantum Information Theory?
Aron C. Wall
Comments: 6 pages, 2 figures. Additional references added to arxiv version
Journal-ref: Proc. 28th Solvay Conf. Phys., ed. D. Gross, A. Sevrin, P. Zoller, World Scientific Publishing Co., Singapore, 2023
Subjects: General Relativity and Quantum Cosmology (gr-qc); High Energy Physics - Theory (hep-th)
I suggest the possibility that holographic quantum gravity is, in some sense, equivalent to quantum information theory. Some radical implications would follow. First, the theory of quantum gravity should have no adjustable coupling constants, similar to string theory. Thus, all complete bulk theories of quantum gravity are dual to each other. By setting up an appropriately entangled state, it should be possible to find wormholes connecting any two quantum gravity theories (e.g. string theory and loop quantum gravity). Secondly, if we represent space at one time as a tensor network, then dynamics is automatically encoded via gauge-equivalent descriptions of the boundary state. This would appear to imply, contrary to semiclassical expectations, that a closed universe should have only one state.
except
Last edited by a moderator: