Is My Double Integral Solution Correct?

[harpazo]

I must evaluate the following double integral over the region R. I do not understand the limits of integration given the following equations.

Let S S = double integral symbol

S S x dx dy

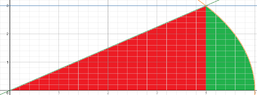
Limits of integration for x:

From (4y/3) to sqrt{25 - y^2}.

Note: Why is the variable y in the radicand? Shouldn't it be sqrt{25 - x^2}?

Limits of integration for y:

From 0 to 3.

I was able to reduced the double integral to a single integral S.

S [(25 - y^2)y]/2 - [(8y^2)/9]y dy from 0 to 3.

My answer is 225/8.

The textbook answer is simply 25.

Is the textbook answer correct? If so, why?

 

[MarkFL]

This is how I would evaluate the given integral:

$$I=\int_0^3 \int_{\frac{4}{3}y}^{\sqrt{25-y^2}} x\,dx\,dy$$

$$I=\frac{1}{2}\int_0^3 (25-y^2)-\left(\frac{16}{9}y^2\right)\,dy$$

$$I=\frac{25}{18}\int_0^3 9-y^2\,dy$$

$$I=\frac{25}{54}\left[27y-y^3\right]_0^3=\frac{25}{54}\cdot54=25$$

 

[harpazo]

This is how I would evaluate the given integral:

$$I=\int_0^3 \int_{\frac{4}{3}y}^{\sqrt{25-y^2}} x\,dx\,dy$$

$$I=\frac{1}{2}\int_0^3 (25-y^2)-\left(\frac{16}{9}y^2\right)\,dy$$

$$I=\frac{25}{18}\int_0^3 9-y^2\,dy$$

$$I=\frac{25}{54}\left[27y-y^3\right]_0^3=\frac{25}{54}\cdot54=25$$

Can you show me how to integrate this same function over dydx?

 

[MarkFL]

Can you show me how to integrate this same function over dydx?

Sure, so what we need to do here is examine the region $D$ over which we are integrating...which can be expressed by the inequalities:

$$0\le y\le3$$

$$\frac{4}{3}y\le x\le\sqrt{25-y^2}$$

Now, in order to reverse the order in integration, we will have to break $D$ up into two regions as follows:

View attachment 6548

$$I=\int_0^4 x\int_0^{\frac{3}{4}x}\,dy\,dx+\int_4^5 x\int_0^{\sqrt{25-x^2}}\,dy\,dx$$

$$I=\frac{3}{4}\int_0^4 x^2\,dx+\int_4^5 x\sqrt{25-x^2}\,dx$$

$$I=\frac{1}{4}\left[x^3\right]_0^4+\frac{1}{2}\int_0^9 u^{\frac{1}{2}}\,du$$

$$I=16+\frac{1}{3}9^{\frac{3}{2}}=16+9=25$$

 

[harpazo]

Sure, so what we need to do here is examine the region $D$ over which we are integrating...which can be expressed by the inequalities:

$$0\le y\le3$$

$$\frac{4}{3}y\le x\le\sqrt{25-y^2}$$

Now, in order to reverse the order in integration, we will have to break $D$ up into two regions as follows:
$$I=\int_0^4 x\int_0^{\frac{3}{4}x}\,dy\,dx+\int_4^5 x\int_0^{\sqrt{25-x^2}}\,dy\,dx$$

$$I=\frac{3}{4}\int_0^4 x^2\,dx+\int_4^5 x\sqrt{25-x^2}\,dx$$

$$I=\frac{1}{4}\left[x^3\right]_0^4+\frac{1}{2}\int_0^9 u^{\frac{1}{2}}\,du$$

$$I=16+\frac{1}{3}9^{\frac{3}{2}}=16+9=25$$

Brilliantly done! Why two integrals for dydx and not dxdy?

 

[MarkFL]

Brilliantly done! Why two integrals for dydx and not dxdy?

Well, if you look at the region $D$, you can see that integrating in the original order (with horizontal segments), the left and right bounds of each segment are along the same curves all the way up from $y=0$ to $y=3$, but reversing the order and using vertical segments, we have the same bottom boundary from $x=0$ to $x=5$, but the upper boundary is one curve on $0\le x\le4$ and another curve from $4\le x\le 5$. And so to integrate in that order, we must use 2 integrals. :D

 

[harpazo]

Well, if you look at the region $D$, you can see that integrating in the original order (with horizontal segments), the left and right bounds of each segment are along the same curves all the way up from $y=0$ to $y=3$, but reversing the order and using vertical segments, we have the same bottom boundary from $x=0$ to $x=5$, but the upper boundary is one curve on $0\le x\le4$ and another curve from $4\le x\le 5$. And so to integrate in that order, we must use 2 integrals. :D

I thank you for your great help with the set up. I will be posting more double integrals. I have trouble deciding if dxdy is better to use or dydx for certain questions.

In fact, I am having trouble finding the limits of integration for double integrals. I am also having trouble setting up the integrals. I will post 3 questions that involve setting up the double integrals. No need to integrate the double integral just the set up.

 

[Prove It]

I thank you for your great help with the set up. I will be posting more double integrals. I have trouble deciding if dxdy is better to use or dydx for certain questions.

In fact, I am having trouble finding the limits of integration for double integrals. I am also having trouble setting up the integrals. I will post 3 questions that involve setting up the double integrals. No need to integrate the double integral just the set up.

To decide, do a sketch of your region, and draw in both horizontal and vertical strips. If one way can be done without the lower and upper boundaries changing, then choose that one.

 

[harpazo]

Thank you everyone.