Is My Homework Solution Correct?

[Pushoam]

Homework Statement

Homework Equations

The Attempt at a Solution

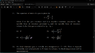
$C_p - C_v = p \frac{\partial V}{\partial T}$
Doing the above, I got $R\{ 1+ \frac{bp} {RT^2}\}$, there is no square in the right factor.
I want to know whether my answer is correct.

 

[Chestermiller]

$C_p - C_v = p \frac{\partial V}{\partial T}$

This equation is incorrect.

 

[Pushoam]

This equation is incorrect.

How is it so?
$C_p = [\frac{\partial U}{\partial T} = C_v] +p \frac{\partial V}{\partial T}$
Isn't the above correct?
Will you please reply to the following threads,too?
Which cylinder reaches the ground first?

2nd order differential eqn.

Material: semi - conductor or metal?

 

[Chestermiller]

How is it so?
$C_p = [\frac{\partial U}{\partial T} = C_v] +p \frac{\partial V}{\partial T}$
Isn't the above correct?
Will you please reply to the following threads,too?
Which cylinder reaches the ground first?

2nd order differential eqn.

Material: semi - conductor or metal?

No. That equation is not correct. Consult your textbook for the correct equation for determining the difference between the two heat capacities.

 

[Pushoam]

C_p = [\frac{\partial U}{\partial T} = C_v] +p \frac{\partial V}{\partial T}

$\frac{\partial U}{\partial V} \frac{\partial V}{\partial T} = \frac{\partial U}{\partial T} = C_v$
How to calculate the above as U is not given?

Sorry, the above is wrong as V and T are independent variables?
U is a fn. of both V and T. Then, how to calculate $\frac{\partial U}{\partial V}$?

 

[Chestermiller]

View attachment 214682
C_p = [\frac{\partial U}{\partial T} = C_v] +p \frac{\partial V}{\partial T}

$\frac{\partial U}{\partial V} \frac{\partial V}{\partial T} = \frac{\partial U}{\partial T} = C_v$
How to calculate the above as U is not given?

Sorry, the above is wrong as V and T are independent variables?
U is a fn. of both V and T. Then, how to calculate $\frac{\partial U}{\partial V}$?

That should be in your book also.

 

[Pushoam]

That should be in your book also.

I didn't get it in the book.
I took U = pV and expressed p in terms of V.
This gives, p = $\frac {RT}{V + \frac b T }$
This gives $U = RT - \frac {bR}{V + \frac b T } \\ \frac { \partial U} {\partial V} = \frac {bR}{\{V + \frac b T\}^2 }$
After doing further calculation,
we get the option c as the correct answer.
But how to prove that U = pV? Is it valid always?

 

[Chestermiller]

I didn't get it in the book.
I took U = pV and expressed p in terms of V.
This gives, p = $\frac {RT}{V + \frac b T }$
This gives $U = RT - \frac {bR}{V + \frac b T } \\ \frac { \partial U} {\partial V} = \frac {bR}{\{V + \frac b T\}^2 }$
After doing further calculation,
we get the option c as the correct answer.
But how to prove that U = pV? Is it valid always?

It's not even valid for an ideal gas.

 

[Pushoam]

It's not even valid for an ideal gas.

Which part is not valild? Is it U = pV?
But, it gave the correct answer.

 

[Charles Link]

I was able to show with some work by expanding differentials of $U(T,P)$ and $U(T,V)$ that $C_P-C_V=P \big( \frac{\partial{V}}{\partial{T}} \big)_P +\big( \frac{\partial{U}}{\partial{P}} \big)_T \big( \frac{\partial{P}}{\partial{T}} \big)_V$. I don't know, however, how to compute $\big( \frac{\partial{U}}{\partial{P}} \big)_T$ from the information provided.

 

[Chestermiller]

Which part is not valild? Is it U = pV?

If you're going to wild ass it like this, I won't be helping you any more. Now, I'll give you one more opportunity: What does your book give as the general expression for the partial derivative of U with respect to V at constant T.

But, it gave the correct answer.

So what!

 

[Chestermiller]

I was able to show with some work by expanding differentials of $U(T,P)$ and $U(T,V)$ that $C_P-C_v=P( \frac{\partial{V}}{\partial{T}})_P +(\frac{\partial{U}}{\partial{P}})_T (\frac{\partial{P}}{\partial{T}})_V$. I don't know, however, how to compute $(\frac{\partial{U}}{\partial{P}})_T$ from the information provided.

All thermo books give a general expression in terms of P, V, and T for this partial derivative.

 

[Abhishek kumar]

Which part is not valild? Is it U = pV?
But, it gave the correct answer.

Which part is not valild? Is it U = pV?
But, it gave the correct answer.[/Q

Which part is not valild? Is it U = pV?
But, it gave the correct answer.

First

I didn't get it in the book.
I took U = pV and expressed p in terms of V.
This gives, p = $\frac {RT}{V + \frac b T }$
This gives $U = RT - \frac {bR}{V + \frac b T } \\ \frac { \partial U} {\partial V} = \frac {bR}{\{V + \frac b T\}^2 }$
After doing further calculation,
we get the option c as the correct answer.
But how to prove that U = pV? Is it valid always?

Apply this formula you will get the result

 

[Charles Link]

Thank you @Chestermiller :) I usually try to solve these (thermodynamic problems) without looking the necessary equation up in a textbook, but this one is a little more difficult. Adkins book, Equilibrium Thermodynamics, gives equation (8.4): $C_P-C_V=T \big( \frac{\partial{P}}{\partial{T}} \big)_V \big( \frac{\partial{V}}{\partial{T}} \big)_P$. $\\$ The rest was simply applying some calculus with a little algebra. (Yes, I was able to get the correct answer). $\\$ @Pushoam may also find this equation to be helpful.

 

[Chestermiller]

Thank you @Chestermiller :) I usually try to solve these (thermodynamic problems) without looking the necessary equation up in a textbook, but this one is a little more difficult. Adkins book, Equilibrium Thermodynamics, gives equation (8.4): $C_P-C_V=T \big( \frac{\partial{P}}{\partial{T}} \big)_V \big( \frac{\partial{V}}{\partial{T}} \big)_P$. $\\$ The rest was simply applying some calculus with a little algebra. (Yes, I was able to get the correct answer). $\\$ @Pushoam may also find this equation to be helpful.

Hi Charles,
I just gave another member a warning for revealing essentially what you revealed in this post, since it is essentially the complete solution. I was hoping that the OP would do research on his own to find the relationship (or the derivative of U with respect to V at constant T) in order to discourage him from making wild guesses. I suppose I'll cancel the other member's warning if I can figure out how to.

Chet

 

[Charles Link]

Hi Charles,
I just gave another member a warning for revealing essentially what you revealed in this post, since it is essentially the complete solution. I was hoping that the OP would do research on his own to find the relationship (or the derivative of U with respect to V at constant T) in order to discourage him from making wild guesses. I suppose I'll cancel the other member's warning if I can figure out how to.

Chet

Hello @Chestermiller If you are referring to post 13, it is interesting, but he doesn't show the origin of his equation, and I believe it to be incorrect. It is also dimensionally incorrect, if I'm not mistaken.

 

[Charles Link]

Apply this formula you will get the result

For the OP @Pushoam and @Abhishek kumar I believe this equation (post 13) is incorrect. See my post 14. I think the equation in post 13 is not even dimensionally correct.

 

[Chestermiller]

For the OP @Pushoam and @Abhishek kumar I believe this equation (post 13) is incorrect. See my post 14. I think the equation in post 13 is not even dimensionally correct.

Sorry to say this Charles, but I agree with the result in post #13. It is essentially the same as your result in post #14.

 

[Charles Link]

Sorry to say this Charles, but I agree with the result in post #13. It is essentially the same as your result in post #14.

My mistake with the dimensional analysis. It's going to take a little work to show the two are equivalent though.

 

[Chestermiller]

My mistake with the dimensional analysis. It's going to take a little work to show the two are equivalent though.

V=V(P,T)
dV = ??
then, set dV = 0

 

[Charles Link]

V=V(P,T)
dV = ??
then, set dV = 0

I just got the result. It's easier than I thought it would be. Will show it momentarily... $\\$ $dP=\big( \frac{\partial{P}}{\partial{T}} \big)_V dT+\big( \frac{\partial{P}}{\partial{V}} \big)_T dV$. Setting $dP=0$ allows one to take $\big( \frac{\partial{V}}{\partial{T}} \big)_P$. The hardest part was actually writing out the Latex. :)

 

[Abhishek kumar]

V=V(P,T)
dV = ??
then, set dV = 0

Dear Chestermiller posting correct formula is not allowed?i haven't posted complete solution how can you warn me?

 

[Charles Link]

Dear Chestermiller posting correct formula is not allowed?i haven't posted complete solution how can you warn me?

Please see his post #15. I can't speak for him, but I think he changed his mind. He might not have been able to cancel it.

 

[Chestermiller]

Dear Chestermiller posting correct formula is not allowed?i haven't posted complete solution how can you warn me?

Please see my message to you in a private conversation.

 

[Pushoam]

If you're going to wild ass it like this, I won't be helping you any more. Now, I'll give you one more opportunity: What does your book give as the general expression for the partial derivative of U with respect to V at constant T.So what!

I have to find out $C_P - C_V = \{\frac{\partial U} {\partial V} +p\}\frac{dV}{dT}$

For $C_V$, I have to calculate $\frac{\partial U} {\partial T}$. It is not needed to calculate $C_V$ for this problem,

but this gives me the idea that here, U is a function of two variables V and T.

Not getting how to calculate $\frac{\partial U} {\partial V}$ from dU = T dS - pdV, I thought of using Maxwell's relation.

So, I take that potential which is a function of V and T i.e. Helmholtz function F.

F = U - TS

dF = - pdV - S dT

Maxwell's relation gives,

$\frac{\partial F} {\partial T} = -S \\\frac{\partial F} {\partial V}= -p \\ \frac{\partial S} {\partial V}= \frac{\partial p} {\partial T} \\ \frac{\partial U} {\partial V} = \frac{\partial F} {\partial V} + T \frac{\partial S} {\partial V} = -p +T\frac{\partial p} {\partial T}$

Is this correct?

Thank you for discouraging me from Wild guess. Wild guess simply wastes time.Doing further calculation,

$\{\frac{\partial U} {\partial V} +p\} = p\{ 1+ \frac {bp}{RT^2} \}$

$\frac {dV}{dT}= \frac 1 p \{ 1+ \frac {bp}{RT^2} \}$
So, $C_P - C_V = \{\frac{\partial U} {\partial V} +p\}\frac{dV}{dT} = {\{ 1+ \frac {bp}{RT^2} \}}^2$
Here, I have taken U as a function of V and T. So, V and T are independent variables.

While calculating $\frac {dV}{dT}$, I have taken V as a function of T keeping p constant. Isn't it wrong?

Shouldn't I take $\frac {dV}{dT} =0$ assuming U as a function of V and T and so V and T independent variables?

 

[Charles Link]

The derivative $\big( \frac{\partial{V}}{\partial{T}} \big)_P = \frac{dV}{dT}$ should have a factor of $R$ in it. That will give you the correct answer for $C_P-C_V$. $\\$ Note: It's not really $\frac{ dV}{dT}$. $V$ is a function of two other variables=in this case $V=V(T,P )$ . $\\$ You can write $dV=\big( \frac{\partial{V}}{\partial{T}} \big)_P \, dT+ \big(\frac{ \partial{V}}{\partial{P}} \big)_T \, dP$ , but not $\frac{dV}{dT}$.

 

[Pushoam]

The derivative $\big( \frac{\partial{V}}{\partial{T}} \big)_P = \frac{dV}{dT}$ should have a factor of $R$ in it. That will give you the correct answer for $C_P-C_V$.

Yes, it has. Thanks for pointing it out.

 

[Pushoam]

Note: It's not really $\frac{ dV}{dT}$ . V is a function of two other variables=in this case V=V(T,P) You can write $\big( \frac{\partial{V}}{\partial{T}} \big)_P \, dT+ \big(\frac{ \partial{V}}{\partial{P}} \big)_T \, dP$ , but not $\frac{dV}{dT}$ .

Here, I have taken U as a function of V and T. So, V and T are independent variables.

While calculating $\frac {dV}{dT}$ , I have taken V as a function of T keeping p constant. Isn't it wrong?

Shouldn't I take $\frac {dV}{dT} =0$ assuming U as a function of V and T and so V and T independent variables?

What about this?
Sometimes V is independent, sometimes V becomes a fn. of P and T. This I find difficult to understand.

 

[Chestermiller]

I have to find out $C_P - C_V = \{\frac{\partial U} {\partial V} +p\}\frac{dV}{dT}$

For $C_V$, I have to calculate $\frac{\partial U} {\partial T}$. It is not needed to calculate $C_V$ for this problem,

but this gives me the idea that here, U is a function of two variables V and T.

Not getting how to calculate $\frac{\partial U} {\partial V}$ from dU = T dS - pdV, I thought of using Maxwell's relation.

So, I take that potential which is a function of V and T i.e. Helmholtz function F.

F = U - TS

dF = - pdV - S dT

Maxwell's relation gives,

$\frac{\partial F} {\partial T} = -S \\\frac{\partial F} {\partial V}= -p \\ \frac{\partial S} {\partial V}= \frac{\partial p} {\partial T} \\ \frac{\partial U} {\partial V} = \frac{\partial F} {\partial V} + T \frac{\partial S} {\partial V} = -p +T\frac{\partial p} {\partial T}$

Is this correct?

Thank you for discouraging me from Wild guess. Wild guess simply wastes time.

Now, that's what I was looking for. Congratulations. We're proud of you. You've transformed from a wild guesser into a Scholar. Keep up the good work.

 

[Charles Link]

In writing some of the calculations with Latex, for shorthand it can be helpful to write $\frac{dV}{dT}$, but this expression always requires the other variable to be held constant. See my edited post 26. Writing many partial derivatives with Latex is really rather difficult. It would be much easier if we had pencil and paper... To answer post 28, you can write $U=U(T,P)$, and also $U=U(T,V)$. When you write out $dU$, you get two different expressions, (see post 26), one with $dT$ and $dP$ , and the other with $dT$ and $dV$...