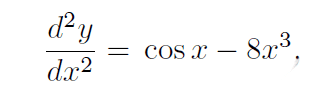
Show us what you got.Student4 said:Can anyone just help me integrate this 2 times. (with maple or somekind math program, or hand). Need to see if my 2 solutions is correct for this one.
View attachment 40636
Integrating a function is a mathematical process that involves finding the area under the curve of the function. It is essentially the reverse process of differentiation, where instead of finding the slope of a curve, we are finding the area under the curve.
Integrating a function is important because it allows us to solve a variety of real-world problems. It is used in physics, engineering, economics, and many other fields to analyze and understand complex systems.
Integrating a function involves using specific mathematical techniques, such as the power rule, substitution, or integration by parts. The exact method depends on the type of function and its complexity.
Definite integration involves finding the value of the area under the curve between two specific points, while indefinite integration involves finding the general antiderivative of a function. In other words, definite integration gives a numerical value, while indefinite integration gives a function.
No, not all functions can be integrated. Functions that are non-continuous or have infinite discontinuities cannot be integrated. In addition, some functions are simply too complex to integrate using standard techniques and may require more advanced methods such as numerical integration.