Is My Product of Sums Equation and NOR Gate Schematic Correct?

[shamieh]

Just need someone to check my work. Couldn't find the problem via Google.

$f$(W,X,Y,Z) M (0,1,2,7,12,15) + d(3,13).

1)Find the minimum Product of Sums equation using a K-Map.

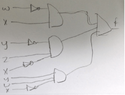
2)Draw a schematic of a minimized circuit implementing the logic using NOR gates.

1) My Answer: $$(\bar{w} + x)(\bar{y} + z + \bar{x})(y + w + \bar{x})$$

2) My Answer: View attachment 1411

 

[Evgeny.Makarov]

I agree with 1). As for 2), NOR can express AND, OR and NOT: see Wikipedia. However, expressing the usual connectives through NOR requires duplication of inputs. For example, PQ (the conjunction of P and Q) equals (P NOR P) NOR (Q NOR Q). If P is itself a big expression, the resulting expression is at least twice as big because P is used two times. So when constructing a circuit, you probably should split the output of P and feed it into both inputs of NOR instead of having two sub-circuits representing P.

 

[shamieh]

on)

Thank you.