EnricoHendro
- 80
- 11
- Homework Statement
- A 4.00-L sample of a diatomic ideal gas with specific heat ratio 1.40, confined to a cylinder, is carried through a closed cycle. The gas is initially at 1.00 atm and 300 K. First, its pressure is tripled under constant volume. Then, it expands adiabatically to its original pressure. Finally, the gas is compressed isobarically to its original volume. (a) Determine the volume of the gas at the end of the adiabatic expansion. (b) Find the temperature of the gas at the start of the adiabatic expansion. (c) Find the temperature at the end of the cycle. (d) What was the net work done on the gas for this cycle?
- Relevant Equations
- PV=nRT
P(V^y) = Constant
Hello there, is my solution for part d logically correct? Here is my attempt at the solution :
Part a :
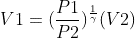
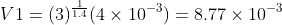
where : P1 = 3P2
Part b :
Since P1=3P2, therefore, T1=3T, where T=300K. Thus, T1=900K
Part c :
Because the final pressure at the end of the cycle is exactly the same as the pressure at the very beginning of the cycle and the volume at the end of the cycle is equal to the very beginning of the cycle, then, T3 = T = 300K, (with T3 = Temperature at the end of the cycle)
Part d :
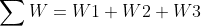
W1 = 0 (Because the first process is isovolumetric)
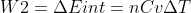 (since the process is adiabatic, where Q=0)
(since the process is adiabatic, where Q=0)
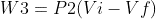 (isobaric process)
(isobaric process)
since :
n is constant assuming no leak and no additional gas during the whole process
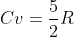
and
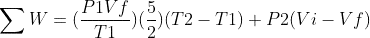
With :
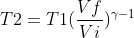
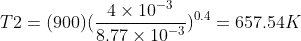
Therefore :
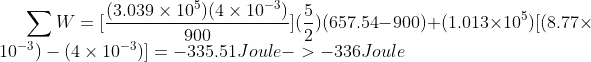
Where,
Vf=V2
Vi=V1
T1=900K
My textbook's answer in part d is also -336Joule, but the method in the solution manual is different than mine.
p.s. The volume is in cubic meter
Thank you
Part a :
where : P1 = 3P2
Part b :
Since P1=3P2, therefore, T1=3T, where T=300K. Thus, T1=900K
Part c :
Because the final pressure at the end of the cycle is exactly the same as the pressure at the very beginning of the cycle and the volume at the end of the cycle is equal to the very beginning of the cycle, then, T3 = T = 300K, (with T3 = Temperature at the end of the cycle)
Part d :
W1 = 0 (Because the first process is isovolumetric)
since :
n is constant assuming no leak and no additional gas during the whole process
and
With :
Therefore :
Where,
Vf=V2
Vi=V1
T1=900K
My textbook's answer in part d is also -336Joule, but the method in the solution manual is different than mine.
p.s. The volume is in cubic meter
Thank you