- #1
Dethrone
- 717
- 0
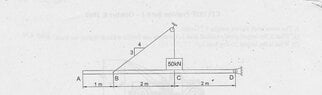
In the structure shown, a cable is attached to the 50 kN weight and to the beam A-D at point B. If the horizontal uniform beam weighs 8 kN/m, determine the following:
(a) The horizontal and vertical component of the force that the pin at D exerts on the beam A-D.
(b) The force in the cable.
...
View attachment 3383
I just want to focus on getting the vertical component right...and I have developed two methods, each of which return a different answer.
1) Taking moments about A (i know doing it about B is simpler):
$$\sum M= T_y -40(2.5)-(T-50)(3)+D_y(5)$$
$$\sum F_y = T_y-40-50+D_y =0$$
$$=T \sin36.9-90+D_y$$
Now solving the two equations, I get $D_y = 61.98 \text{kN}$2) Starting with this line...
$$\sum M_B = -40(1.5)-50(2)-(50-T)(2)+4(V)=0$$
Any of them correct?
(a) The horizontal and vertical component of the force that the pin at D exerts on the beam A-D.
(b) The force in the cable.
...
View attachment 3383
I just want to focus on getting the vertical component right...and I have developed two methods, each of which return a different answer.
1) Taking moments about A (i know doing it about B is simpler):
$$\sum M= T_y -40(2.5)-(T-50)(3)+D_y(5)$$
$$\sum F_y = T_y-40-50+D_y =0$$
$$=T \sin36.9-90+D_y$$
Now solving the two equations, I get $D_y = 61.98 \text{kN}$2) Starting with this line...
$$\sum M_B = -40(1.5)-50(2)-(50-T)(2)+4(V)=0$$
Any of them correct?