I Is Something Missing in the Expansion of Our Flat Universe?

[Apashanka]

From friedmann equation

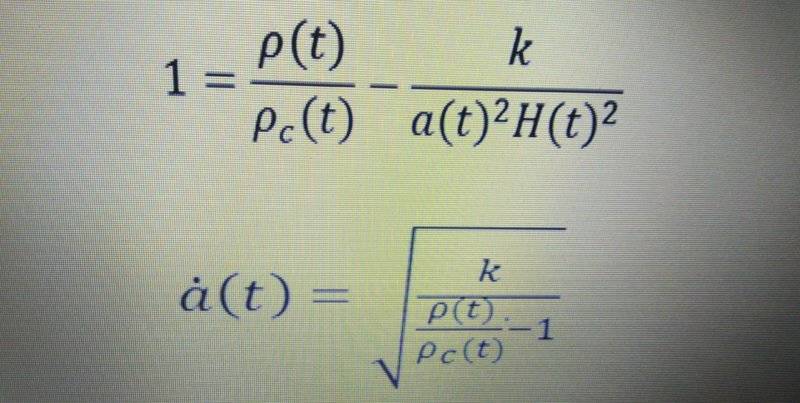
And

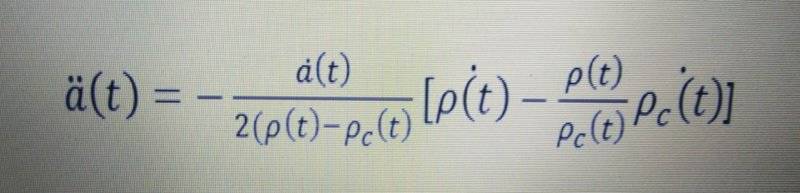For a flat universe with k=0 and ρ=ρ_c ,da/dt becomes undefined and d²a/dt² becomes 0
But for the present time we know that our universe is flat and expanding with a acceleration (q -ve) ,
Therefore is it here something I am missing??

 

[addaF]

Hi,

Precisely $k$ refers to the spatial curvature of our Universe. Actually $k \neq 0$ but It is really close to $0$.
$$
\begin{cases}
k > 0 \quad \text{closed "spherical" universe} \\
k = 0 \quad \text{flat universe} \\
k < 0 \quad \text{open "hyperbolic" universe}
\end{cases}
$$
The set of Universe with $k = 0$ is a $\textbf{null set}$, then the probability of having such Universes is equal to zero. It is not experimentally meaningful to find $k$ precisely $0$, there is always an error bar.

Usually in Friedman equation you can neglect the spatial curvature, but it does not mean that it is precisely $0$

 

[PeterDonis]

From friedmann equation

Where are you getting this from?

 

[PeterDonis]

The set of Universe with k=0 k = 0 is a null set\textbf{null set}, then the probability of having such Universes is equal to zero.

This is true as a matter of actual measurements (we can never measure $k$ to be exactly 0), but irrelevant to the question the OP is asking, because he is claiming that a theoretical model with $k = 0$ is somehow inconsistent. That can be shown to be wrong without considering the measurement aspect at all.

 

[Orodruin]

is a null setnull set\textbf{null set}, then the probability of having such Universes is equal to zero

This is not necessarily true. It is only true if you assume that the probability distribution for k is everywhere finite. It is perfectly fine in probability theory to have probability distributions where the cdf is not continuous, ie, with particular points having a non-zero probability. The set k=0 is null in the standard measure on the real numbers, but that in itself means very little.

 

[Apashanka]

This is not necessarily true. It is only true if you assume that the probability distribution for k is everywhere finite. It is perfectly fine in probability theory to have probability distributions where the cdf is not continuous, ie, with particular points having a non-zero probability. The set k=0 is null in the standard measure on the real numbers, but that in itself means very little.

Sorry I am not in a position to text right now ,I am reposting my question

 

[PeterDonis]

I am reposting my question

My response is still the same: where are you getting this from?

 

[Apashanka]

My response is still the same: where are you getting this from?

From the first Einstein field equation for FRW metric
3H²+3k/a²=8πGρ,little simplification gives the result posted in #6
Where ρ_c is 3H²/8πG(critical density)
(From R₀₀-1/2Rg₀₀)=8πGT₀₀

 

[PeterDonis]

From the first Einstein field equation for FRW metric
3H2+3k/a2=8πGρ,little simplification gives the result posted in #6

Have you considered the possibility that what your "little simplification" implies is not that $\dot{a} = \infty$ for $\rho = \rho_c$ and $k = \pm 1$, but that $k = \pm 1$ is not possible if $\rho = \rho_c$?

 

[Apashanka]

Have you considered the possibility that what your "little simplification" implies is not that $\dot{a} = \infty$ for $\rho = \rho_c$ and $k = \pm 1$, but that $k = \pm 1$ is not possible if $\rho = \rho_c$?

So why is the word 'HALT EXPANSION AFTER INFINITE TIME ' is associated with critical density ??
Is it something related to this

The first one for expansion with acceleration and the second one with linear expansion .
Implies after the time at which ρ=ρ_c , a is not defined ,is it so??
(It is only for k=+-1,k=0 will allow expansion forever)

 

[PeterDonis]

So why is the word 'HALT EXPANSION AFTER INFINITE TIME ' is associated with critical density ??

Please give a specific reference where you are getting all this from. We can't comment on vague statements with no source.

Implies after the time at which ρ=ρc , a is not defined ,is it so??

I've already given you a strong hint in post #9. You need to go back and re-check the math. It doesn't mean what you think it means.

 

[Apashanka]

Please give a specific reference where you are getting all this from. We can't comment on vague statements with no

http://astronomy.swin.edu.au/cosmos/C/Critical+Density

 

[PeterDonis]

http://astronomy.swin.edu.au/cosmos/C/Critical+Density

This gives no math other than the definition of $\rho_c$. Can you show me a source that says "just halt its expansion but only after an infinite time" and gives the math that supports that? "Source" means "textbook or peer-reviewed paper"; you need to be looking at those to get a proper understanding of this issue.

(Hint: if you find such a source, you will find that the math it gives only allows $k = 0$ if $\rho = \rho_c$.)

 

[Apashanka]

This gives no math other than the definition of $\rho_c$. Can you show me a source that says "just halt its expansion but only after an infinite time" and gives the math that supports that? "Source" means "textbook or peer-reviewed paper"; you need to be looking at those to get a proper understanding of this issue.

(Hint: if you find such a source, you will find that the math it gives only allows $k = 0$ if $\rho = \rho_c$.)

Is it that for k=+-1 ,at the time of ρ=ρ_c ,a(t) at that time can't be defined ,that's why it is not allowed ??
But for k=0 ,it will allow expansion or contraction (linear or accelerated) forever...

 

[Orodruin]

As you have been told repeatedly, you cannot have $\rho = \rho_c$ without having $k= 0$ or vice versa. The curvature is directly dependent on the energy content relative to the expansion rate.

There is no such thing as ”the time of $\rho = \rho_c$”. It is either satisfied at all times or it is never satisfied.

 

[Apashanka]

There is no such thing as ”the time of ρ=ρcρ=ρc\rho = \rho_c”. It is either satisfied at all times or it is never satisfied.

Ok if ρ=ρ_c is satisfied for all times , then for k=+-1 , the scale factor can't be defined...and no question of expansion or contraction or static.
Is it??

 

[Orodruin]

Ok if ρ=ρ_c is satisfied for all times , then for k=+-1 , the scale factor can't be defined...and no question of expansion or contraction or static.
Is it??

Really? You are not reading. Reread the statement. You cannot have $k = \pm 1$ when $\rho = \rho_c$ because then $k = 0$ by definition.

 

[PeterDonis]

The OP question has been answered. Thread closed.