Is Taking the Reciprocal a Valid Approach in Differentiating dpH/dV?

[Borek]

I am reading an old paper and I have came to the passage shown in the picture:

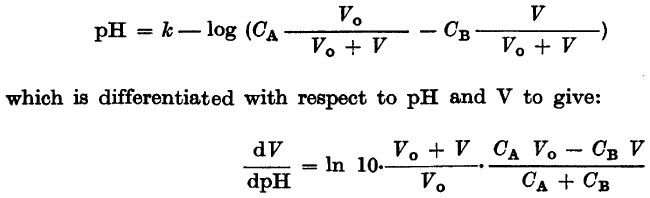
k, C_A, C_B and V₀ are all just some constants.

I think I know what they did - they differentiated the first equation calculating dpH/dV and then took reciprocals of both sides of the equation. Is it a valid approach?

I am not able to get the same result solving the first equation for V and calculating dV/dpH then.

Bear in mind I am mathemathically challenged and English is my second language, I can be missing something obvious.

 

[D H]

Yes, this is a valid approach. Let y=f(x). Obviously, dy/dx = df/dx. Differentiating y=f(x) with respect to y yields

1 = \frac{df}{dx}\,\frac{dx}{dy}

Solving for dx/dy,

\frac{dx}{dy} = \frac 1 {df/dx} = \frac 1 {dy/dx}

 

[Borek]

OK, thank you.

So going the other way (that is solving for V and differentiating), I should get the same result?

 

[epenguin]

OK, thank you.

So going the other way (that is solving for V and differentiating), I should get the same result?

On the way there I think you slightly simplify and easier see the calculation if you combine terms inside the bracket of first eq. into a single fraction and then express that as

pH = k - log(C_AV₀ - C_BV) + log(V₀ + V)

 

[Borek]

I have to solve for V, having two logs doesn't make it easier.

I tried both manually and with TI 89, but I can't get the same result as the one printed. Will try later again.

 

[epenguin]

Borek, I'll put this up here instead of PM as hopefully someone can check it in case of mistakes er typos.

For the differentiation

pH = k - log(\frac{C_AV_0 - C_BV}{V_0 + V})

= k - log(C_AV_0 - C_BV) +log(V_0 + V)

= k + \ln 10 [-\ln(C_AV_0 - C_BV) + \ln(V_0 + V)]

Then differentiating

\frac{dpH}{dV} = [\frac{- C_B}{C_AV_0 - C_BV} + \frac{1}{V_0 + V}].\ln 10

From this you can already see that the point where the LHS is infinite (the pH against V graph is vertical, or V against pH horizontal) is where
V = \frac{V_0C_A}{C_B}.The RHS fractions can be combined giving

[\frac{\ln10.(C_A - C_B)V_0}{(C_AV_0 - C_BV)(V_0 + V)}]

If you wanted to invert this into V = a function of \frac{dV}{dpH}, rearrange to

(C_AV_0 - C_BV)(V_0 + V) = (C_A - C_B)V_0.\ln 10.\frac{dV}{dpH}

call the RHS R, say, and then express V by solving the unlovely quadratic in V:

-V^2C_B + V V_0(C_A - C_B) + (C_A V_0^2 - R) = 0

You ought to get the same thing by inverting and differentiating but I think it is more tedious.

You said you want to invert the first equation anyway. I question whether you do - if it is for plotting it suffices to switch around axes when you plot rather than invert algebraically.

For inverting algebraically work with H rather than pH; and instead of k (which is probably a p something) I define k = - log M, (M = 10^-k)

Then the first equation becomes

H = M + \frac{C_AV_0 - C_BV}{V_0 + V}

which eventually transforms to

V = [\frac{C_A - C_B}{C_B + H - M} + 1]V_0

or in terms of pH and k

V = [\frac{C_A - C_B}{C_B + 10^{-H} - 10^{-k}} + 1]V_0

 

[Borek]

From this you can already see that the point where the LHS is infinite (the pH against V graph is vertical, or V against pH horizontal) is where
V = \frac{V_0C_A}{C_B}.

Hardly surprising - that's the equivalence point

You said you want to invert the first equation anyway.

Whatever I was doing was just to make sure I understand what is going on. And today I had a time to try again - everything is OK.

call the RHS R, say, and then express V by solving the unlovely quadratic in V:

-V^2C_B + V V_0(C_A - C_B) + (C_A V_0^2 - R) = 0

Something is wrong, no need for quadratic here:

V = \frac {-(10^k - C_A 10^{pH}) V_0} {10^k + C_B 10^{pH}}

For inverting algebraically work with H rather than pH

Nah, that's about dV/dpH - volume vs potentiometric answer.

This is from the Gran method original paper, BTW.

k (which is probably a p something)

No, that's log(activity coefficient).

Thank's for the help. Yesterday I was not sure about this reciprocal thing - it seemed logical, but I have learned not to trust my instincts when it comes to anything more complicated than multiplication table.

 

[epenguin]

I will work through it again with more calm and clearer head (also had computer trouble today).
We want to show the students how we make mistakes and are very 'umble.

 

[Redbelly98]

Borek, I'll put this up here instead of PM as hopefully someone can check it in case of mistakes er typos.

For the differentiation

pH = k - log(\frac{C_AV_0 - C_BV}{V_0 + V})

= k - log(C_AV_0 - C_BV) +log(V_0 + V)

= k + \ln 10 [-\ln(C_AV_0 - C_BV) + \ln(V_0 + V)]

Then differentiating

\frac{dpH}{dV} = [\frac{- C_B}{C_AV_0 - C_BV} + \frac{1}{V_0 + V}].\ln 10

Should that be +C_B in the numerator (two minus-signs cancel each other)?