A Is the Assertion Derived from a General Theorem Trivial or Interesting?

  • A
  • Thread starter Thread starter wrobel
  • Start date Start date
wrobel
Science Advisor
Insights Author
Messages
1,139
Reaction score
987
There is an assertion that follows from very general theorem directly and I do not understand if this assertion trivial or it may be of some interest. The assertion is enclosed below please comment
Screenshot_2021-07-14_21-47-43.png
 
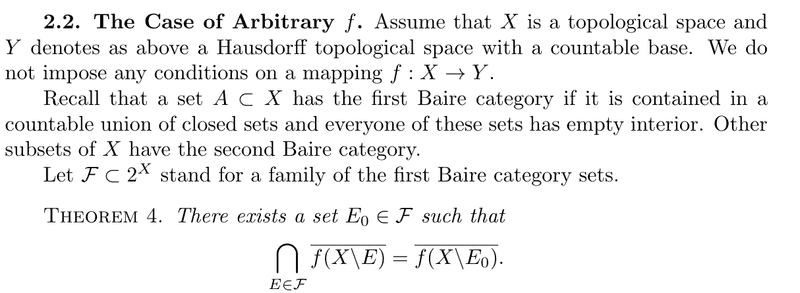
Last edited:

Thread '2-sphere intrinsic definition by gluing disks' boundaries'

A sphere as topological manifold can be defined by gluing together the boundary of two disk. Basically one starts assigning each disk the subspace topology from ##\mathbb R^2## and then taking the quotient topology obtained by gluing their boundaries. Starting from the above definition of 2-sphere as topological manifold, shows that it is homeomorphic to the "embedded" sphere understood as subset of ##\mathbb R^3## in the subspace topology.
View full post »

Similar threads

MHB Operator norm .... Field, Theorem 9.2.9 ....
Replies
2
Views
1K
I Multivariable Analysis .... Directional & Partial Derivatives
Replies
3
Views
2K
MHB Multivariable Analysis .... Directional and Partial Derivatives .... D&K Propostion 2.3.3 ....
Replies
1
Views
1K
MHB Differentiating Vector-Valued Function: Junghenn Prop 9.1.2 - Peter seeks help
Replies
1
Views
1K
I Derivative of a Vector-Valued Function of a Real Variable ...
Replies
8
Views
2K
I On theorem 1.19 in Folland's and completion of measure
Replies
1
Views
2K
B Are Inverse Problems More Complex Than Direct Problems in Mathematics?
Replies
13
Views
3K
I Closure in a Topological Space .... Willard, Theorem 3.7 .... ....
Replies
5
Views
2K
MHB Remarks by Fortney Following Theorems on Directional Derivative ....
Replies
2
Views
1K
MHB Convergence of Geometric Series .... Sohrab, Proposition 2.3.8 .... ....
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top