Is the Backward Euler Method Always A-Stable?

[evinda]

Hello! (Wave)

We have the problem

$$\left\{\begin{matrix}
y'=\lambda y &, t \in [0,+\infty), \lambda \in \mathbb{C}, Re(\lambda)<0 \\
y(0)=1 &
\end{matrix}\right.$$

Applying the Backward Euler method $y^{n+1}=y^n+h \lambda y^{n+1}$, we get that $y^n=\frac{1}{(1-h \lambda)^n}$.

So that the method is stable we require $|y^n|$ to be bounded as $n \to +\infty$.

$$\left| \frac{1}{1-\lambda h}\right| \leq 1 \Rightarrow |1-h \lambda| \geq 1$$Notice that $|1-h \lambda| \geq 1$ since $Re(\lambda) \leq 0$.
Consequently, the region of absolute stability of this method contains the whole left complex semi-plane and so the Backward Euler method is $A-$stable.
Is there no restriction for $h$ for the following reason?

It holds that $|1-h \lambda| \geq 1 \Rightarrow 1-h \lambda \geq 1 \text{ or } 1-h \lambda \leq -1 \\ \Rightarrow -h \lambda \geq 0 \text{ or } -h \lambda \leq -2 \\ \Rightarrow h \lambda \leq 0 \text{ or } h \lambda \geq 2$Could we say that it cannot hold that $h \lambda \geq 2$ since $Re(\lambda) \leq 0$ and so $|1-h \lambda| \geq 1 \Rightarrow h \lambda \leq 0$ which is always true?Also how do we deduce that the region of absolute stability of this method contains the whole left complex semi-plane and so the Backward Euler method is $A-$stable?
We have that $|1-z| \geq 1$, where $z=h \lambda$.

We set $z=x+yi$.

So we have:

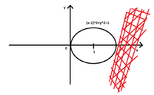
$|1-z| \geq 1 \Rightarrow |1-(x+yi)| \geq 1 \Rightarrow |(1-x)-yi| \geq 1 \Rightarrow (1-x)^2+y^2 \geq 1$.
View attachment 4335Why isn't the red marked region the region of absolute stability but the whole left complex semi-plane?

 

[jvicens]

Hello there! I can provide some clarification for your questions.

Firstly, you are correct in saying that there is no restriction for $h$ in this method. This is because the inequality $|1-h \lambda| \geq 1$ holds for all values of $h$ and $\lambda$ in the given conditions. So, we cannot say that $h\lambda \leq 0$ is always true, as there may be cases where $h\lambda \geq 2$. However, we can say that $h\lambda \leq 0$ is always true for $Re(\lambda) \leq 0$.

Moving on to your second question, the reason why the region of absolute stability of this method contains the whole left complex semi-plane is because of the inequality $|1-h \lambda| \geq 1$. This inequality holds for all values of $h$ and $\lambda$ in the given conditions, which means that the method is stable for all values in this region. The red marked region is just an example of a possible region of absolute stability, but it is not the only one. The whole left complex semi-plane is also a valid region of absolute stability, as it satisfies the inequality and ensures stability of the method.

I hope this helps clarify your doubts. Let me know if you have any further questions. Happy researching!