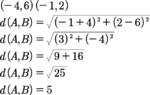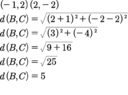Is the distance between AB and BC the same using the given coordinates?

[mathdad]

Given A(-4, 6), B(-1, 2), and C(2, -2), show that AB = BC.

Can I use the distance formula in this case?

 

[MarkFL]

Yes, the distance formula would work, or if you can show the 3 points are collinear, then you could use the mid-point formula. :)

 

[mathdad]

Yes, the distance formula would work, or if you can show the 3 points are collinear, then you could use the mid-point formula. :)

Can you show me your way?

 

[mathdad]

I decided to find AB first.

View attachment 7381

 

[MarkFL]

Can you show me your way?

In order for three points to be collinear, we can pick any two distinct sets of two points from the set of three to form two line segments, and those two line segments will have the same slope if the three points are collinear.

What are the slopes of the line segments $\overline{AB}$ and $\overline{BC}$ ?

 

[mathdad]

Here is distance BC.

View attachment 7382

- - - Updated - - -

Ok. I see that AB = BC.

 

[MarkFL]

Please attach the images inline...otherwise they won't show up in the "Topic Review" and having them show up there can be helpful when replying to a thread. Please see this thread:

http://mathhelpboards.com/questions-comments-feedback-25/attachment-image-line-21253.html

for instructions on posting attached images inline. :)

 

[mathdad]

Let m = slope

(-4,6) and (-1,2)

m(AB) = (2-6)/(-1-(-4))

m(AB) = (-4)/(-1+4)

m(A,B) = -4/3

(-1,2) and (2,-2)m(BC) = (-2-2)/(2-(-1))

m(BC) = (-4)/(2+1)

m(BC) = -4/3

I see that m(AB) = m(BC).

What does this tell me?

 

[mathdad]

Please attach the images inline...otherwise they won't show up in the "Topic Review" and having them show up there can be helpful when replying to a thread. Please see this thread:

http://mathhelpboards.com/questions-comments-feedback-25/attachment-image-line-21253.html

for instructions on posting attached images inline. :)

This does not work for me. I do not have a computer. I tried several times. It let's me select from my files but does not me upload the selected image.

I use my cell phone for all my internet work. I honestly do not have a computer in my room. What is wrong with uploading images by MathMagic Lite as I have been doing so far.

 

[MarkFL]

Let m = slope

(-4,6) and (-1,2)

m(AB) = (2-6)/(-1-(-4))

m(AB) = (-4)/(-1+4)

m(A,B) = -4/3

(-1,2) and (2,-2)m(BC) = (-2-2)/(2-(-1))

m(BC) = (-4)/(2+1)

m(BC) = -4/3

I see that m(AB) = m(BC).

What does this tell me?

It tells you the three points are collinear...now, is point $B$ the midpoint of $\overline{AC}$ ?

This does not work for me. I do not have a computer. I tried several times. It let's me select from my files but does not me upload the selected image.
I use my cell phone for all my internet work. I honestly do not have a computer in my room. What is wrong with uploading images by MathMagic Lite as I have been doing so far.

 

[mathdad]

How can I tell if point B is the midpoint of line segment AC?

 

[MarkFL]

How can I tell if point B is the midpoint of line segment AC?

Use the midpoint formula with the endpoints of $\overline{AC}$ and see if the resulting coordinates match those of point $B$. :)

Suppose the three given points were not collinear...can you think of a plan that would still allow you to use the midpoint formula?

 

[mathdad]

From now on, no more than two math questions whenever I decide to visit the MHB. I feel that less questions per visit leads to a more thorough reply and discussion per question.

 

[MarkFL]

As a follow-up to everything I posted, let's first find the mid-point $\left(x_M,y_M\right)$ of $\overline{AC}$:

$$\left(x_M,y_M\right)=\left(\frac{-4+2}{2},\frac{6+(-2)}{2}\right)=(-1,2)$$

This is point $B$ and so we know:

$$\overline{AB}=\overline{BC}$$

Now, suppose we have two points in the plane, points $A=\left(x_A,y_A\right)$ and $C=\left(x_C,y_C\right)$. Now, the locus of all points $B=\left(x_B,y_B\right)$ equidistant from both $A$ and $C$ can be found by using the distance formula:

$$\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2=\left(x_B-x_C\right)^2+\left(y_B-y_C\right)^2$$

Expand:

$$x_B^2-2x_Ax_B+x_A^2+y_B^2-2y_Ay_B+y_A^2=x_B^2-2x_Bx_C+x_C^2+y_B^2-2y_By_C+y_C^2$$

Combine like terms:

$$-2x_Ax_B+x_A^2-2y_Ay_B+y_A^2=-2x_Bx_C+x_C^2-2y_By_C+y_C^2$$

Arrange linear equation in point-slope form:

$$y_B-\frac{y_A+y_C}{2}=\frac{x_C-x_A}{y_C-y_A}\left(x_B-\frac{x_A+x_C}{2}\right)$$

As we should expect, we see this is the line perpendicular to the segment $\overline{AC}$ and passing through the midpoint of $\overline{AC}$. (Yes)

 

[mathdad]

Mark:

Wonderful job!