chikchok
- 7
- 0
- TL;DR Summary
- Fermi-Dirac distribution
I`m sorry if this seems too obvious, just trying to clarify something. When Fermi-Dirac distribution is equal to zero , can we assume it is the state of
the highest energy? (Because the propability of occupation is zero)
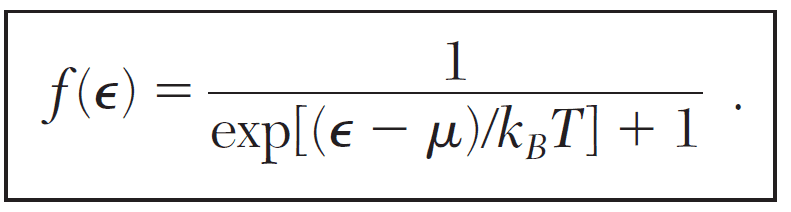
the highest energy? (Because the propability of occupation is zero)