- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Is the FLRW Metric a Valid Approximation for Our Universe on Large Scales?
- A
- Thread starter Tanujhm
- Start date
-
- Tags
- Metric
In summary: The Robertson-Walker-Metric is an exact solution to the Einstein field equations if the universe is inhomogeneous and has perfect homogeneity and isotropy everywhere. However, this metric is only valid under a universe with those conditions. Additionally, the metric eliminates the need for dark energy and other theories related to it.
Space news on Phys.org
- #2
- 22,278
- 13,888
The signature of the metric is purely conventional. Different sources will use different convention. This goes for all metrics, not just the RW metric.
Edit: You are probably used to sources with +—- signature and reading a source with -+++ signature.
Edit: You are probably used to sources with +—- signature and reading a source with -+++ signature.
- #3
- 22,278
- 13,888
Ah no wait:
This
This
is not true regardless of convention for the standard form of those metrics. Please state your sources.Tanujhm said:Summary: FLRW
despite Minkowskis, Schwarzschilds and Kerrs
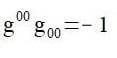
- #4
Tanujhm
- 2
- 0
Right, my fault.Orodruin said:Ah no wait:
This
is not true regardless of convention for the standard form of those metrics. Please state your sources.
- #5
Ibix
Science Advisor
- 12,568
- 14,690
The value of ##g_{00}g^{00}## will depend on your choice of coordinates, even in a given spacetime. With a diagonal metric, though, ##g_{00}=1/g^{00}## and the product is always 1.
Are you asking why some sources have an overall minus sign with respect to others? That is, some sources quote ##g_{tt}=1## and some ##g_{tt}=-1## in FLRW, or ##g_{tt}=1-2GM/c^2r## and some ##-(1-2GM/c^2r)## in Schwarzschild spacetime? If so, it's just the metric signature - you will find all the components have swapped sign. It makes no difference to anything measurable, but you do need to be careful combining formulae from different sources because if they use different conventions you can find inconsistent signs.
Are you asking why some sources have an overall minus sign with respect to others? That is, some sources quote ##g_{tt}=1## and some ##g_{tt}=-1## in FLRW, or ##g_{tt}=1-2GM/c^2r## and some ##-(1-2GM/c^2r)## in Schwarzschild spacetime? If so, it's just the metric signature - you will find all the components have swapped sign. It makes no difference to anything measurable, but you do need to be careful combining formulae from different sources because if they use different conventions you can find inconsistent signs.
- #6
- 22,278
- 13,888
... and the metric signature is not the only sign convention so beware of the others too!Ibix said:if they use different conventions you can find inconsistent signs
- #7
Dragrath
- 47
- 42
As others have said the choice of sign convention is arbitrary as long as you are consistent in FLRW metric. That said there is an important and underappreciated caveat regarding the FLRW metric and that is it is only an exact solution under a universe with perfect homogeneity and isotropy everywhere. There is an alarming fallacious tendency in cosmology to assume that you can approximate a universe under the FLRW metric if you have sufficiently small deviations from perfect isotropy such that you can treat the universe as uniform ans isotropic at large scales but this would require a violation of the conservation of information which must hold mathematically for any system of partial differential equations since by definition there must be a unique solution for all possible valid initial conditions. Or basically since information is defined in terms of what you need to perfectly describe the state of a system the only way a universe can be treated as isotropic and homogenous at any scale is if there is either no information contained within the Universe i.e. the trivial null state. For any other solution off diagonal elements of the metric tensor will always fail to cancel out perfectly for any mathematically valid solution to the Einstein field equations. This also nicely explains why the FLRW metric remains the only known exact solution to the general Einstein field equations.
Based on the work by Matthew Kleban and Leonardo Senatore in Inhomogenous and anisotropic cosmology (Matthew Kleban and Leonardo Senatore JCAP10(2016)022) it can be shown that within the limiting case of any non trivial flat or open universe which is initially expanding these asymmetries in the off diagonal terms will always drive a net expansion for any arbitrary choice of initial conditions (including the choice of lambda or cosmological constant) these anisotropic off diagonal components will always lead to a net expansion of the Universe. Through using a proof by contradiction they show that the conditions needed for the overall net expansion to stop can never be met because they require two mutually incompatible conditions neither of which can ever be satisfied thus no valid solutions can exist to the Einstein field equations which lead to any big crunch scenarios in any initially expanding nontrivial flat or open cosmology.
The point of the above is that we have already mathematically falsified the validity of FLRW based cosmology by showing it requires the violation of information conservation making any such solutions mathematically invalid.
That isn't to say FLRW is useless after all one reason FLRW cosmology was chosen over a century ago is it is simple and it needs to be remembered that they had no general use computers (analog computers designed for specific problems did exist) which could run the full nonlinear anisotropic and inhomogenous solutions as computers were a profession back then not a machine. Nowadays we have amassed more than enough observational proof to falsify the cosmological principal (Nathan J. Secrest et al 2021 ApJL 908 L51) as well as theoretical reasons for why the cosmological principal must always be violated yet in cosmology FLRW is still taken as gospel in the form of Lambda CDM cosmology.
As a bonus this also eliminates the entire Hubble tension, the need for so called dark energy to explain the observed net acceleration of expansion, the axis of evil problem and shows how al of thermodynamics and the arrow of time naturally emerge within the Einstein field equations as Universal constraints on the metric tensor at least in the limiting case of any initially expanding nontrivial flat or open universe.
FLRW is a useful tool for learning GR but I feel it needs to be emphasized that our universe can not obey a FLRW metric. A meta mathematical approach applying definitions and axioms is likely the best way to see why this is an inescapable conclusion. The point of this is once you add these complexities into the equations I suspect the sign convention will take on a different importance as the off diagonal terms become more important.
https://iopscience.iop.org/article/10.1088/1475-7516/2016/10/022/meta
https://iopscience.iop.org/article/10.3847/2041-8213/abdd40
Based on the work by Matthew Kleban and Leonardo Senatore in Inhomogenous and anisotropic cosmology (Matthew Kleban and Leonardo Senatore JCAP10(2016)022) it can be shown that within the limiting case of any non trivial flat or open universe which is initially expanding these asymmetries in the off diagonal terms will always drive a net expansion for any arbitrary choice of initial conditions (including the choice of lambda or cosmological constant) these anisotropic off diagonal components will always lead to a net expansion of the Universe. Through using a proof by contradiction they show that the conditions needed for the overall net expansion to stop can never be met because they require two mutually incompatible conditions neither of which can ever be satisfied thus no valid solutions can exist to the Einstein field equations which lead to any big crunch scenarios in any initially expanding nontrivial flat or open cosmology.
The point of the above is that we have already mathematically falsified the validity of FLRW based cosmology by showing it requires the violation of information conservation making any such solutions mathematically invalid.
That isn't to say FLRW is useless after all one reason FLRW cosmology was chosen over a century ago is it is simple and it needs to be remembered that they had no general use computers (analog computers designed for specific problems did exist) which could run the full nonlinear anisotropic and inhomogenous solutions as computers were a profession back then not a machine. Nowadays we have amassed more than enough observational proof to falsify the cosmological principal (Nathan J. Secrest et al 2021 ApJL 908 L51) as well as theoretical reasons for why the cosmological principal must always be violated yet in cosmology FLRW is still taken as gospel in the form of Lambda CDM cosmology.
As a bonus this also eliminates the entire Hubble tension, the need for so called dark energy to explain the observed net acceleration of expansion, the axis of evil problem and shows how al of thermodynamics and the arrow of time naturally emerge within the Einstein field equations as Universal constraints on the metric tensor at least in the limiting case of any initially expanding nontrivial flat or open universe.
FLRW is a useful tool for learning GR but I feel it needs to be emphasized that our universe can not obey a FLRW metric. A meta mathematical approach applying definitions and axioms is likely the best way to see why this is an inescapable conclusion. The point of this is once you add these complexities into the equations I suspect the sign convention will take on a different importance as the off diagonal terms become more important.
https://iopscience.iop.org/article/10.1088/1475-7516/2016/10/022/meta
https://iopscience.iop.org/article/10.3847/2041-8213/abdd40
- #8
PeterDonis
Mentor
- 47,601
- 23,876
I don't understand what you are trying to say here. Using an exact FLRW metric as an approximation for our actual universe on large scales is not the same as claiming that the exact FLRW metric you are using is an exact solution for more than one set of initial conditions. It's just an approximation.Dragrath said:There is an alarming fallacious tendency in cosmology to assume that you can approximate a universe under the FLRW metric if you have sufficiently small deviations from perfect isotropy such that you can treat the universe as uniform ans isotropic at large scales but this would require a violation of the conservation of information which must hold mathematically for any system of partial differential equations since by definition there must be a unique solution for all possible valid initial conditions.
If you are talking about the question of whether the exact FLRW metric is a valid approximation for our universe on large scales, there have been plenty of papers published questioning that and proposing alternative approaches, although my understanding is that none of those have gained traction in the mainstream cosmology community. Which is not to say that no such alternatives ever will.
I have no idea where you are getting this from. There are many other exact solutions known:Dragrath said:the FLRW metric remains the only known exact solution to the general Einstein field equations
https://en.wikipedia.org/wiki/Exact_solutions_in_general_relativity#Types_of_exact_solution
Do you mean this paper?Dragrath said:Matthew Kleban and Leonardo Senatore JCAP10(2016)022
https://iopscience.iop.org/article/10.1088/1475-7516/2016/10/022/meta
This claim is much too strong; see my comments above. I don't think the paper you reference supports it either, particularly since the only scenario that paper claims to rule out, the "Big Crunch", is not part of our best current model of our universe anyway.Dragrath said:The point of the above is that we have already mathematically falsified the validity of FLRW based cosmology by showing it requires the violation of information conservation making any such solutions mathematically invalid.
Do you mean this paper?Dragrath said:Nathan J. Secrest et al 2021 ApJL 908 L51
https://iopscience.iop.org/article/10.3847/2041-8213/abdd40/meta
This claim is much too strong as well. See my remarks above about approximation.Dragrath said:Nowadays we have amassed more than enough observational proof to falsify the cosmological principal (Nathan J. Secrest et al 2021 ApJL 908 L51) as well as theoretical reasons for why the cosmological principal must always be violated yet in cosmology FLRW is still taken as gospel in the form of Lambda CDM cosmology.
FAQ: Is the FLRW Metric a Valid Approximation for Our Universe on Large Scales?
What is the Robertson-Walker metric?
The Robertson-Walker metric is a mathematical framework used to describe the geometry of the universe in the context of general relativity. It is a solution to Einstein's field equations and is used to model the expansion of the universe.
How is the Robertson-Walker metric derived?
The Robertson-Walker metric is derived from the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric, which is a generalization of the Friedmann equations. It takes into account the curvature of space and the expansion of the universe.
What are the assumptions made in the Robertson-Walker metric?
The Robertson-Walker metric assumes that the universe is homogeneous and isotropic, meaning that it is the same in all directions and at all points in space. It also assumes that the universe is expanding, but not accelerating.
How is the Robertson-Walker metric used in cosmology?
The Robertson-Walker metric is used to describe the large-scale structure of the universe and to make predictions about its evolution. It is also used to calculate important quantities such as the Hubble parameter and the scale factor, which are used in cosmological models.
Are there any limitations to the Robertson-Walker metric?
While the Robertson-Walker metric is a useful tool in cosmology, it has some limitations. It does not take into account the effects of dark energy, dark matter, or gravitational waves, which are important factors in the evolution of the universe. It also assumes a flat universe, which may not be accurate for our actual universe.
Similar threads
- Replies
- 6
- Views
- 2K
- Replies
- 1
- Views
- 5K
- Replies
- 9
- Views
- 2K
- Replies
- 6
- Views
- 3K
- Replies
- 27
- Views
- 4K
- Replies
- 4
- Views
- 3K
- Replies
- 8
- Views
- 2K
- Replies
- 13
- Views
- 2K
- Replies
- 24
- Views
- 4K
Share:
