- #1
Jus10
- 12
- 2
So the main reason I'm posting about this problem is that one of the teaching assistants helped me with this problem, but a buddy of mine got something different on part A and part B (Assess). So I wanted to post up here and see what you guys say.
1. Homework Statement
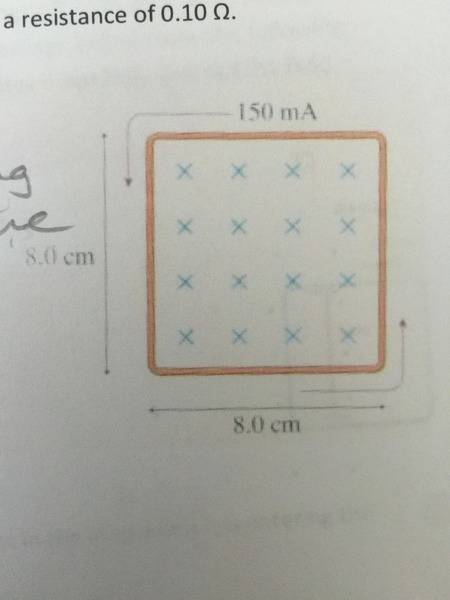
The loop in the figure has an induced current as shown. The loop as a resistance of 0.10Ω.
Part A) Is the magnetic field strength increasing or decreasing? Explain how you determined your answer.
Part B) What is the rate of change of the field ΔB/Δt?
(Prepare)
(Solve)
(Asses) How would your answers change if the drawn current direction were reversed?
ε=IR
ε=(ΔB/Δt)A
Part A) The applied field is decreasing because the flux is out of the page & the current is counter-clockwise.
Part B) (Prepare) I = 0.15 A
R = 0.10 Ω
A = 6.4e-3
(Solve) ε = (0.15)(0.10)
ε = 0.015 V
0.015 = (ΔB/Δt)(6.4e-3)
ΔB/Δt = 0.015/6.4e-3
ΔB/Δt = 2.34 T/s
(Assess) If the current were reversed, the applied field would be INCREASING. So, instead of DECREASING by 2.34 T/s, it would INCREASE by 2.34 T/s
1. Homework Statement
The loop in the figure has an induced current as shown. The loop as a resistance of 0.10Ω.
Part A) Is the magnetic field strength increasing or decreasing? Explain how you determined your answer.
Part B) What is the rate of change of the field ΔB/Δt?
(Prepare)
(Solve)
(Asses) How would your answers change if the drawn current direction were reversed?
Homework Equations
ε=IR
ε=(ΔB/Δt)A
The Attempt at a Solution
Part A) The applied field is decreasing because the flux is out of the page & the current is counter-clockwise.
Part B) (Prepare) I = 0.15 A
R = 0.10 Ω
A = 6.4e-3
(Solve) ε = (0.15)(0.10)
ε = 0.015 V
0.015 = (ΔB/Δt)(6.4e-3)
ΔB/Δt = 0.015/6.4e-3
ΔB/Δt = 2.34 T/s
(Assess) If the current were reversed, the applied field would be INCREASING. So, instead of DECREASING by 2.34 T/s, it would INCREASE by 2.34 T/s
Last edited: