Lancelot1
- 26
- 0
Good morning (or evening),
I have a geometrical tricky question, which I need your assistance with.
Look at the following sketch:
View attachment 6574
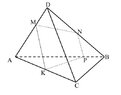
In the sketch you see a pyramid ABCD. Inside the space of ABCD, you see a plane MKPN, where M, K, P and N are points on the pyramid sides.
Using the axioms of geometry in plane and space, I wish to determine if this object is possible or impossible.
I thank you in advance !
I have a geometrical tricky question, which I need your assistance with.
Look at the following sketch:
View attachment 6574
In the sketch you see a pyramid ABCD. Inside the space of ABCD, you see a plane MKPN, where M, K, P and N are points on the pyramid sides.
Using the axioms of geometry in plane and space, I wish to determine if this object is possible or impossible.
I thank you in advance !