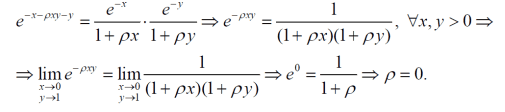- #1
cdux
- 188
- 0
Teacher wanted to prove that for that condition to be satisfied ρ must be zero, but the limits give the idea that it applies only when those limits are satisfied. By the way, x>0 and y>0. Is it a universal proof or only for those limits?