Is the Work Done by a Variable Force Non-Conservative?

[haruspex]

That's worrying. If you do try that be careful not to use θ for both purposes. Either take the polar coordinates to be (r,φ) or change the given parameter from θ to t, say. I say it is worrying because it makes me wonder whether your teacher has blundered.

Thank you but what do you mean by this ?! I didn't understand.

View attachment 317261
This one should be Theta ...

No, neither of them matches the given theta. The one you circled would give $x=r\cos(\theta), y=r\sin(\theta), y/x=\tan(\theta)$. But you are given $y/x= \frac 12\cot(\theta)$.
If you draw a line from the origin to a point half way along the horizontal dashed blue line, the angle between that and the y-axis is the given theta.

 

[MatinSAR]

If you are going from A to C, the limits of integration are from $\theta=0$ to $\theta = \frac{\pi}{2}$. From the equations for F and dr that I gave in post #16, what is the equation for F dotted with dr?

Is it true ?!

Forget $\theta$ as a variable. Try this. You have $$x=2a\sin\theta~;~~2y=2a\cos\theta.$$It follows that $$x^2+4y^2=4a^2 \implies xdx+4ydy=0 \implies dx=-\frac{4y}{x}dy$$ Now $$\mathbf{F}\cdot d\mathbf{r}=(x^2y~\mathbf{\hat x}+xy^2~\mathbf{\hat y})\cdot(dx~\mathbf{\hat x}+dy~\mathbf{\hat y})
=x^2ydx+xy^2dy.$$ Substitute the expression for $dx$ and integrate over $y$.

Can I send a picture of my work ?! The final answer is unusual ...

 

[MatinSAR]

That's worrying. If you do try that be careful not to use θ for both purposes. Either take the polar coordinates to be (r,φ) or change the given parameter from θ to t, say. I say it is worrying because it makes me wonder whether your teacher has blundered.

No, neither of them matches the given theta. The one you circled would give $x=r\cos(\theta), y=r\sin(\theta), y/x=\tan(\theta)$. But you are given $y/x= \frac 12\cot(\theta)$.
If you draw a line from the origin to a point half way along the horizontal dashed blue line, the angle between that and the y-axis is the given theta.

Thanks ...
Is it true ?!

 

[kuruman]

Can I send a picture of my work ?! The final answer is unusual ...

LaTeX is preferable, but if your work is too involved, you can post a picture as long as it is clearly legible and right side up. Use the "Attach files" link, lower left.

 

[haruspex]

Is it true ?!
View attachment 317282

I don't get the factor as 6. Did you handle the signs correctly? The rest looks fine.

 

[MatinSAR]

LaTeX is preferable, but if your work is too involved, you can post a picture as long as it is clearly legible and right side up. Use the "Attach files" link, lower left.

Thank you ... I have done it with a math editor.

 

[MatinSAR]

I don't get the factor as 6. Did you handle the signs correctly? The rest looks fine.

What about Theta ?! Did I specify theta correctly?
I get the factor 6 again ! Let me send a picture ...

 

[MatinSAR]

I don't get the factor as 6. Did you handle the signs correctly? The rest looks fine.

 

[erobz]

I'm getting what you are getting.

$$ \int 3 x y^2 dy = \int 3 \cdot y^2 \cdot 2 \sqrt{a^2 - y^2} dy $$

Let:

$\frac{y}{a} = \sin \beta$
$\frac{ \sqrt{a^2 - y^2} }{a} = \cos \beta$

It follows that

$$ y^2 = a^2 \sin^2 \beta$$
$$\sqrt{a^2 - y^2} = a \cos \beta$$
$$ dy = a \cos \beta d \beta$$

$$ \implies \int 3 x y^2 dy = 6 a^4 \int \sin^2 \beta \cos^2 \beta d \beta $$

 

[Chestermiller]

I don't get the factor as 6. Did you handle the signs correctly? The rest looks fine.

I also get a factor of 6, although I would never have done the math the way that he did it>

 

[MatinSAR]

I also get a factor of 6, although I would never have done the math the way that he did it>

Was it true ?!
What was wrong with the way I have done the math

I'm getting what you are getting.

Can you please tell me what is your final answer ?!

 

[erobz]

Was it true ?!
What was wrong with the way I have done the math

Can you please tell me what is your final answer ?!

I didn't do the integral!

 

[erobz]

Post your work, it will get checked by someone...

 

[haruspex]

What about Theta ?! Did I specify theta correctly?
I get the factor 6 again ! Let me send a picture ...

Yes, my mistake… I should have waited until I had the time to check properly.

 

[MatinSAR]

Post your work, it will get checked by someone...

 

[haruspex]

View attachment 317296

It is a line integral, not a double integral, so you must arrange that there is only one variable in the integrand. If you want to do it as an integral wrt y then you must first replace all the occurrences of x with what x is as a function of y.
But really, the parametric approach using theta is much easier.

 

[erobz]

View attachment 317296

Show the work. Explain how you get the last result?

 

[MatinSAR]

It is a line integral, not a double integral, so you must arrange that there is only one variable in the integrand. If you want to do it as an integral wrt y then you must first replace all the occurrences of x with what x is as a function of y.
But really, the parametric approach using theta is much easier.

So my answer is wrong , isn't it ?!
Thank you ... I will try to do it using parametric approach and I will send a picture of the work ...

Show the work. Explain how you get the last result?

Thank you ... I will try to do it using parametrich approach and I will send a picture of the work ...

 

[haruspex]

I will try to do it using parametric approach

I'm confused. Isn’t that what you already did in post #32? Except that you did not perform the integral.

 

[Chestermiller]

The integration is very simple. It just involves the use of trigonometric identities.$$(\sin{\theta}\cos{\theta})^2=\frac{\sin^2{2\theta}}{4}=\frac{1-\cos{4\theta}}{8}$$

 

[Steve4Physics]

View attachment 317296

Hi @MatinSAR. Can I point out a fundamental mistake you are making? I don’t think anyone has mentioned it yet (apologies if they already have).

The final expression for W can not contain x or y (or θ). These are variables which change as you move along the path. They must disappear when the definite integral is evaluated.

You made the same mistake in your Post #1 solution, where your final expression for W contained x and y.

The expression for W can contains only given constants (here only the 'a') and pure numbers like 5, π and √2 (just picking random values as examples).

For example, if you determine the formula for the circumference of a circle, x²+y²=a², it wouldn’t make sense to have x and/or y in the final formula.

 

[MatinSAR]

I'm confused. Isn’t that what you already did in post #32? Except that you did not perform the integral.

Yes. It was unfinished.

The integration is very simple. It just involves the use of trigonometric identities.$$(\sin{\theta}\cos{\theta})^2=\frac{\sin^2{2\theta}}{4}=\frac{1-\cos{4\theta}}{8}$$

Thank you.

Hi @MatinSAR. Can I point out a fundamental mistake you are making? I don’t think anyone has mentioned it yet (apologies if they already have).

The final expression for W can not contain x or y (or θ). These are variables which change as you move along the path. They must disappear when the definite integral is evaluated.

You made the same mistake in your Post #1 solution, where your final expression for W contained x and y.

The expression for W can contains only given constants (here only the 'a') and pure numbers like 5, π and √2 (just picking random values as examples).

For example, if you determine the formula for the circumference of a circle, x²+y²=a², it wouldn’t make sense to have x and/or y in the final formula.

Thank you ... I didn't know about this.

 

[MatinSAR]

I hope it's finally true ...

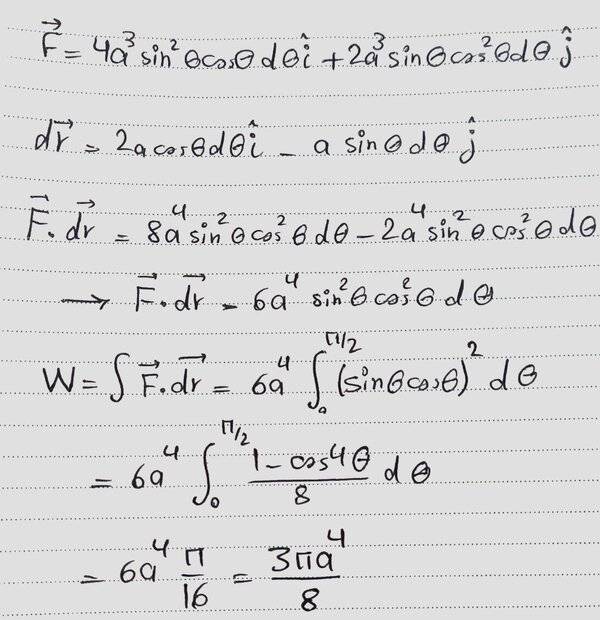The force is conserative so If I choose another path the final answer shouldn't change, Is it true ?!

 

[haruspex]

The force is conserative

Is it? What do you get if you integrate from 0 to 2π?

I agree with your answer.

 

[MatinSAR]

Is it?

It was mentioned in question.

I agree with your answer.

Thank you.

 

[MatinSAR]

.

.

.

.

.

.

I hope I haven't forgotten anyone.

Thank you for your help and time.

 

[haruspex]

It was mentioned in question.

Try the path along the axes. Isn't F always zero there?

 

[MatinSAR]

Try the path along the axes. Isn't F always zero there?

No it's not.

 

[Steve4Physics]

No it's not.

Oh yes it is! (If you familiar with British pantomime.)

Can I expand on what @haruspex said in Post #57?

Referring to the Post #21 diagram, suppose you take the following route:
- from A(0,a), move along the y-axis to the origin (0,0);
- from the origin (0,0) move along the x-axis to C(2a,0).

$\vec F = x^2y~\hat i + xy^2 \hat~j$

While moving along the y-axis (x=0); both components of $\vec F$ are zero.
Similarly while moving along the x-axis.

The total work done along this path is therefore zero. This is different to your calculated value for the original route from A to C.

So you can see (without doing any maths) that the force is not conservative.

 

[MatinSAR]

Referring to the Post #21 diagram, suppose you take the following route:
- from A(0,a), move along the y-axis to the origin (0,0);
- from the origin (0,0) move along the x-axis to C(2a,0).

Great !
So it's not conserative ...
Thank you.