Is the Work Function of Graphene Equal to the Binding Energy?

[schniefen]

Homework Statement

See the attached image.

Relevant Equations

The theory section on ARPES on Wikipedia: https://en.wikipedia.org/wiki/Angle-resolved_photoemission_spectroscopy#Theory

Consider the attached screenshot. The work function of graphene is assumed to be 4.5 eV.

1. Does the work function correspond to the binding energy $E_B$ as given on Wikipedia? What is $E$ in $E−E_F$ in the graph on the right?
2. "...the Fermi level at the K-point..."; is this the point $E=E_F$ above K in the graph on the right?
3. "...the second Brillouin zone K-point..."; which point is this in the two pictures?

 

[member 553083]

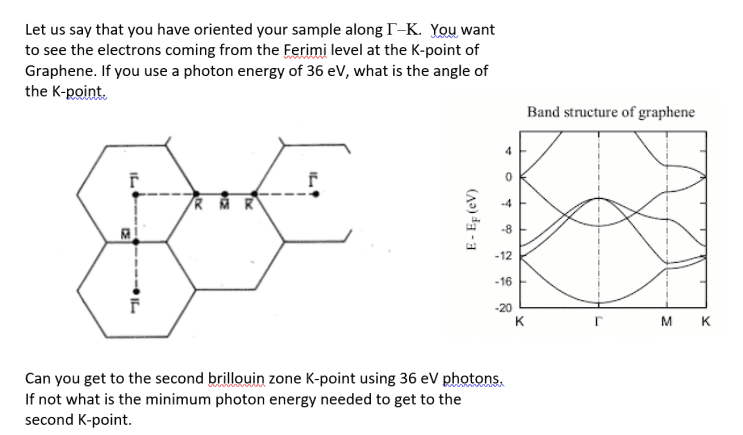
1. No, the work function does not correspond to the binding energy $E_B$ as given on Wikipedia. The work function is related to the binding energy, but is not equal to it. $E$ in $E − E_F$ in the graph on the right is the energy at a particular point in the Brillouin zone, which is not necessarily the Fermi level.2. Yes, this is the point $E = E_F$ above K in the graph on the right.3. The second Brillouin zone K-point is the point labeled K in the plot on the left.