erobz
Gold Member
- 4,445
- 1,839
Let say a package is entering a conveyor belt (velocity ##w##) at zero initial velocity ##v## in the direction of the conveyor.
Initially the package slips as its being accelerated (from rest) to conveyor belt speed. A linear drag force seems reasonable to me for a model:
$$ \beta( \mu, N ) ( w - v ) = m \frac{dv}{dt} $$
##\beta## has dependency on ##\mu## (which has dependency on the relative velocity), and the normal force ##N##, such that ##\beta## is dimensionally consistent. However, if we ignore that for a moment( assuming ##\beta## is a constant) you get the following solution for ##v(t)##:
$$ v(t) = w \left( 1 - e^{-\frac{\beta}{m} t } \right)$$
The problem, with ##\beta## as some constant (if its a problem?) is in this simplification, the package never quite reaches belt speed... it just becomes arbitrarily close to ##w## as ##t \to \infty##:
If we address the fact that ## \beta## is not constant by examining a plot of ##\mu## vs ## (w-v)##: it should look something like this:
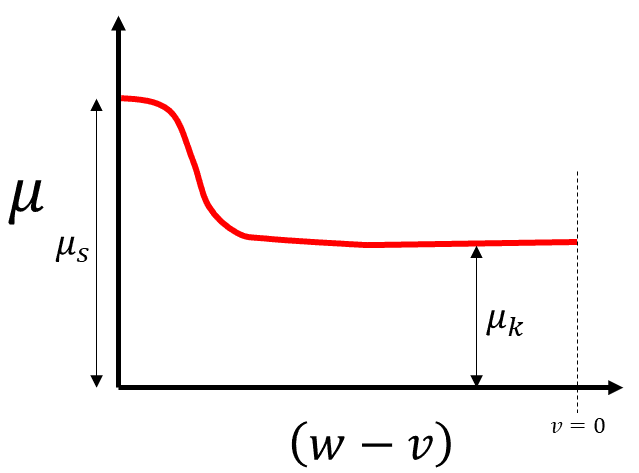
The question I have is if you were to formulate that function for ##\beta## using the characteristics of ##\mu## above would it fix the issue of the package reaching belt speed in finite time, because it at least seems to do so in reality?
Initially the package slips as its being accelerated (from rest) to conveyor belt speed. A linear drag force seems reasonable to me for a model:
$$ \beta( \mu, N ) ( w - v ) = m \frac{dv}{dt} $$
##\beta## has dependency on ##\mu## (which has dependency on the relative velocity), and the normal force ##N##, such that ##\beta## is dimensionally consistent. However, if we ignore that for a moment( assuming ##\beta## is a constant) you get the following solution for ##v(t)##:
$$ v(t) = w \left( 1 - e^{-\frac{\beta}{m} t } \right)$$
The problem, with ##\beta## as some constant (if its a problem?) is in this simplification, the package never quite reaches belt speed... it just becomes arbitrarily close to ##w## as ##t \to \infty##:
If we address the fact that ## \beta## is not constant by examining a plot of ##\mu## vs ## (w-v)##: it should look something like this:
The question I have is if you were to formulate that function for ##\beta## using the characteristics of ##\mu## above would it fix the issue of the package reaching belt speed in finite time, because it at least seems to do so in reality?