- #1
MissP.25_5
- 331
- 0
Is there any other easier way to get the answer for no. 2?
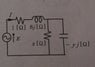
Power supply voltage E=8+4j [V]; Current I=1-j [A].
1) Find the power factor of the circuit as seen from the power supply.
2)Find the values of x and y.
There's a little mistake at the very last part of my working, but anyways, I want to know if there is an easier way.
Power supply voltage E=8+4j [V]; Current I=1-j [A].
1) Find the power factor of the circuit as seen from the power supply.
2)Find the values of x and y.
There's a little mistake at the very last part of my working, but anyways, I want to know if there is an easier way.
Attachments
Last edited: