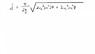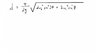- #1
goochmawn314
- 12
- 0
Idk if anyone has figured this out, but I believe I've found a new equation for the length of an arc traveled by, say, a football.
I uploaded a picture of it. I don't have any experimental proof for it, but I used tricky mathematical manipulations with standard projectile equations, the perimeter of an ellipse, and the Pythagorean theorem. Do you think this could get published? Sorry if I sound like a noob
I uploaded a picture of it. I don't have any experimental proof for it, but I used tricky mathematical manipulations with standard projectile equations, the perimeter of an ellipse, and the Pythagorean theorem. Do you think this could get published? Sorry if I sound like a noob