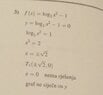Callmelucky
- 144
- 30
- Homework Statement
- Write the coordinates of points where ##f(x)=\log _{2} x^2 -1## intersects x and y axis
- Relevant Equations
- ##\log _{a} x^n = n\times \log _{a} x##
So basically this is how I solved this problem:
1. ##f(x)=\log _{2} x^2 - 1##
2. ##0=\log _{2} x^2 -1 ##
3. ##1= 2\times \log _{2} x##
4. ##\frac{1}{2}= \log _{2} x##
5. ##2^{\frac{1}{2}}=x=\sqrt{2}##
So I wrote coordinates to be (##\sqrt{2}##, 0)
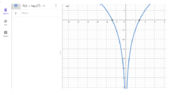
But apparently, that is not the only solution. There should be another answer with a negative sign so (##\pm\sqrt{2}##, 0) would be a complete solution for points at which graphs cross the x line. There are no points where the graph crosses the y-line.
This is how it's solved in the textbook(pic in attachments). And I understand that it's correct because the graph really does cross the x-line in those points.
So, my question is, is there a rule I am not aware of that states that I can't divide an equation with n(exponent of an argument moved down to the front)?
Thank you.
1. ##f(x)=\log _{2} x^2 - 1##
2. ##0=\log _{2} x^2 -1 ##
3. ##1= 2\times \log _{2} x##
4. ##\frac{1}{2}= \log _{2} x##
5. ##2^{\frac{1}{2}}=x=\sqrt{2}##
So I wrote coordinates to be (##\sqrt{2}##, 0)
But apparently, that is not the only solution. There should be another answer with a negative sign so (##\pm\sqrt{2}##, 0) would be a complete solution for points at which graphs cross the x line. There are no points where the graph crosses the y-line.
This is how it's solved in the textbook(pic in attachments). And I understand that it's correct because the graph really does cross the x-line in those points.
So, my question is, is there a rule I am not aware of that states that I can't divide an equation with n(exponent of an argument moved down to the front)?
Thank you.
Attachments
Last edited: