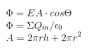- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Is There Flux Through the Lateral Surface of a Cylinder?
In summary, the conversation discusses the correct expression for the area when calculating Φ0 and the formula for the particular area in question. It also mentions the parts of the surface of the cylinder that have nonzero flux, which are the flat ends. The correct expression for the lateral area of the cylinder is also mentioned.
Physics news on Phys.org
- #2
TSny
Science Advisor
Homework Helper
Gold Member
2023 Award
- 14,586
- 4,645
Your expressions for the areas don't look correct. When calculating ##\Phi_0##, what particular area are you working with? What is the formula for this particular area ?
- #3
- #4
TSny
Science Advisor
Homework Helper
Gold Member
2023 Award
- 14,586
- 4,645
Which parts of the surface of the cylinder have nonzero flux?
- #5
Fatima Hasan
- 319
- 14
The area that we're concerned will be the surface area of the ends of Gaussian surface which is equals to π / R^2TSny said:Which parts of the surface of the cylinder have nonzero flux?
Φ = E A = Q enclosed / ε
Q enclosed = ## 100 * π * (0.1)^2 * 8.85 = 27.8 pC ##
Last edited:
- #6
TSny
Science Advisor
Homework Helper
Gold Member
2023 Award
- 14,586
- 4,645
Of course you mean π⋅R^2.Fatima Hasan said:The area that we're concerned will be the surface area of the ends of Gaussian surface which is equals to π / R^2
This is correct.Φ = E A = Q enclosed / ε
Q enclosed = 100 * π * (0.1)^2 * 8.85 = 27.8 pC
- #7
Fatima Hasan
- 319
- 14
##A = 2 \pi r h## , we use this formula to find the net flux through a cylinder , right ?TSny said:Of course you mean π⋅R^2.
This is correct.
Last edited:
- #8
TSny
Science Advisor
Homework Helper
Gold Member
2023 Award
- 14,586
- 4,645
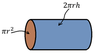
Not in this problem. The area ##A = 2 \pi r h## is the "lateral" area of the curved surface of the cylinder, as shown below in blueFatima Hasan said:##A = 2 \pi r h## , we use this formula to find the net flux through a cylinder , right ?
Is there any flux through the blue surface in the problem you are working on?
Attachments
- #9
Fatima Hasan
- 319
- 14
NoTSny said:Not in this problem. The area ##A = 2 \pi r h## is the "lateral" area of the curved surface of the cylinder, as shown below in blue
View attachment 221399
Is there any flux through the blue surface in the problem you are working on?
FAQ: Is There Flux Through the Lateral Surface of a Cylinder?
What is net charge inside a cylinder?
Net charge inside a cylinder refers to the overall electric charge present within the cylindrical volume. It takes into account both the positive and negative charges present inside the cylinder and calculates the difference between them.
How is net charge inside a cylinder calculated?
The net charge inside a cylinder can be calculated by adding up the individual charges present inside the cylinder. The charges can be either positive or negative, and their magnitude and location must be taken into account when calculating the net charge.
What factors affect the net charge inside a cylinder?
The net charge inside a cylinder can be affected by various factors such as the number and distribution of charges, the distance between the charges, and the electric field strength inside the cylinder. Other factors such as the material of the cylinder and the presence of other objects nearby can also affect the net charge.
What is the significance of net charge inside a cylinder?
The net charge inside a cylinder is significant because it determines the electric field strength inside the cylinder and can affect the behavior of charged particles within the cylinder. It is also a crucial factor in understanding the overall electric potential and capacitance of the cylinder.
How is the net charge inside a cylinder used in practical applications?
The net charge inside a cylinder is used in various practical applications such as in the design of capacitors, in the study of electromagnetic fields, and in the development of electronic devices. It is also a crucial concept in understanding the behavior of charged particles in cylindrical structures, which is relevant in fields such as plasma physics and material science.
Similar threads
- Replies
- 7
- Views
- 1K
- Replies
- 16
- Views
- 466
- Replies
- 7
- Views
- 3K
- Replies
- 1
- Views
- 3K
- Replies
- 10
- Views
- 10K
- Replies
- 2
- Views
- 2K
- Replies
- 4
- Views
- 3K
- Replies
- 10
- Views
- 5K
- Replies
- 9
- Views
- 8K
- Replies
- 10
- Views
- 4K
Share: