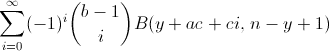chamilka said:
Hi everyone!
I have got this series in a part of my research. I need to check if this is a convergent series and if so, what is the radius of the convergence?
Here is the series..
\[\sum_{i=0}^{\infty}(-1)^{i}{b-1\choose i}B(y+ac+ci,\,n-y+1)\]
Sorry if my LateX code is not visible( I am currently learning LaTeX as said in the Forum rules), see the attached image below!
View attachment 225
Here, a,b and c are any three positive real numbers and y=0,1,2,...n
Thank you for your kind support!
Hi chamilka, :)
Firstly I think you should review what a
power series is. The given series is not a power series and the
radius of convergence is defined only for power series.
\[\sum_{i=0}^{\infty}(-1)^{i}{b-1\choose i}B(y+ac+ci,\,n-y+1)\]
Using the method that we have used http://www.mathhelpboards.com/threads/1358-Chamilka-s-Question-from-Math-Help-Forum?p=6494#post6494, this series can be expressed as the following integral.
\begin{eqnarray}
\sum_{i=0}^{\infty}(-1)^{i}{b-1\choose i}B(y+ac+ci,\,n-y+1)&=&\int_{0}^{1}x^{y+ac-1}(1-x)^{n-y}(1-x^c)^{b-1}\,dx\\
&=&\int_{0}^{1}x^{y+ac-1}\left(\sum_{j=0}^{n-y}(-1)^{j}{n-y\choose j}x^{j}\right)(1-x^c)^{b-1}\,dx\\
&=&\sum_{j=0}^{n-y}\int_{0}^{1}x^{y+ac+j-1}(-1)^{j}{n-y\choose j}(1-x^c)^{b-1}\,dx\\
&=&\sum_{j=0}^{n-y}\int_{0}^{1}(-1)^{j}{n-y\choose j}(x^c)^{\left(\frac{y}{c}+a+\frac{j}{c}-\frac{1}{c}\right)}(1-x^c)^{b-1}\,dx\\
&=&\sum_{j=0}^{n-y}(-1)^{j}{n-y\choose j}\int_{0}^{1}(x^c)^{\left(\frac{y}{c}+a+\frac{j}{c}-\frac{1}{c}\right)}(1-x^c)^{b-1}\,dx\\
\end{eqnarray}
Let, \(\displaystyle x=z^{\frac{1}{c}}\Rightarrow dx=\frac{1}{c}z^{\frac{1}{c}-1}\,dz\)
\begin{eqnarray}
\therefore\sum_{i=0}^{\infty}(-1)^{i}{b-1\choose i}B(y+ac+ci,\,n-y+1)&=&\sum_{j=0}^{n-y}(-1)^{j}{n-y\choose j}\int_{0}^{1}z^{\left(\frac{y}{c}+a+\frac{j}{c}-\frac{1}{c}\right)}(1-z)^{b-1}\frac{1}{c}z^{\frac{1}{c}-1}\,dz\\
&=&\frac{1}{c}\sum_{j=0}^{n-y}(-1)^{j}{n-y\choose j}\int_{0}^{1}z^{\left(\frac{y}{c}+a+\frac{j}{c}-1\right)}(1-z)^{b-1}\,dz\\
&=&\frac{1}{c}\sum_{j=0}^{n-y}(-1)^{j}{n-y\choose j}B\left(\frac{y}{c}+a+\frac{j}{c},\,b\right)
\end{eqnarray}
\(\sum_{j=0}^{n-y}(-1)^{j}{n-y\choose j}B\left(\frac{y}{c}+a+\frac{j}{c},\,b\right)\) is a finite series since, \(n-y\in\mathbb{Z}^{+}\cup\{0\}\)
Therefore, \(\sum_{i=0}^{\infty}(-1)^{i}{b-1\choose i}B(y+ac+ci,\,n-y+1)\) can be written as a finite series and hence it is convergent.
Kind Regards,
Sudharaka.
