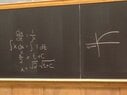- #1
MermaidWonders
- 112
- 0
Question - True or False: If $\frac{dx}{dt}$ = $\frac{1}{x}$ and $x$ = 3 when $t$ = 0, then $x$ is an increasing function of $t$.
View attachment 8011
I understand how the graph of $x$ was obtained (the graph on the board), but I really don't understand why she attempted to draw the negative root of $x$ the way she did in those faint dash lines (if you can see them, they actually try to show a the function $-x$). In other words, why is the $-x$ function a reflection in the $y$-axis of function $x$? Why isn't it reflected in the $x$-axis?
View attachment 8011
I understand how the graph of $x$ was obtained (the graph on the board), but I really don't understand why she attempted to draw the negative root of $x$ the way she did in those faint dash lines (if you can see them, they actually try to show a the function $-x$). In other words, why is the $-x$ function a reflection in the $y$-axis of function $x$? Why isn't it reflected in the $x$-axis?