Ising model autocorrelation function calculation

[yklee]

Homework Statement

on going

Relevant Equations

$$c(t) = \langle A(t'+t) A(t) \rangle - \langle A \rangle^{2} = \frac{1}{t_{max}-t}\sum_{t'=0}^{t_{max}-t} A(t'+t)A(t) - \frac{1}{t_{max}-t}\sum_{t'=0}^{t_{max}-t}A(t'+t) \cdot \frac{1}{t_{max}-t} \sum_{t'=0}^{t_{max}-t}A(t)$$

Dear Mr. and Ms.,

I am trying to measure the autocorrelation functions of 2D ising model based on the equation given by

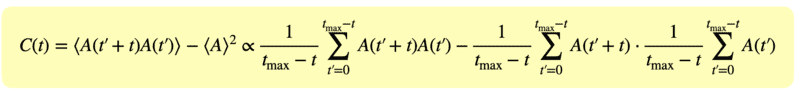
where A(t) denote a measure. I calculate a c(t) of magnetization. I calculated in this way

[CODE lang="python" title="acf"] data_path = f"../../trajectory/data.txt"
data = np.loadtxt(data_path)
Nsteps = len(data)
acf = np.zeros(Nsteps, float)
acf[0] = 1.000
for t in range(1,Nsteps):
value = np.mean(data[t:Nsteps]*data[:Nsteps-t]) - np.mean(data[t:Nsteps])*np.mean(data[:Nsteps-t])
act[t] = value[/CODE]

However, the results seems not good. Can you discuss the wrong part of my calculation?

 

[scottdave]

What is the act[] array? Everything else is acf. I am guessing this is a typo when you entered it here, as this should throw an error.

Other than that - a quick look at your code appears like it should replicate your formula.

Try running this on a small set of data, first - something that you could verify the result of. Then you can scale up to the full data.