It works but why? (Matching experimental data to a random equation)

[adriandwor]

TL;DR Summary

A random equation matches experimental values, but why?

Hey guys,

I've about a week left to submit my final paper for my trade degree in transportation.

The paper is about an analysis of potential implementation of an electric car for direct deliveries in my area where I live.
In part of it, I try to analyze how many possible trips a car like that could have a day and from that deduce potential yearly earnings.
I have about 5000 data points of trips in the area that cover 1 year span.

Data looks something like this:

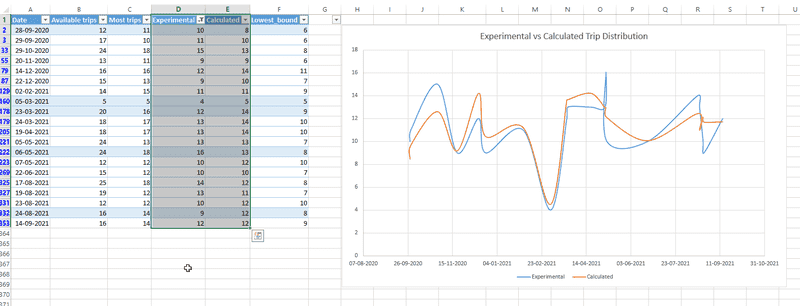
Experimental are trips that have been arranged manually according to the data. Calculated is where I used a formula:

Sqrt ((Available trips - Lowest_bound) +Overlap_Factor) + Lowest_bound

It seems to come very close to the actual number of trips an electric car can have on that day but I don't understand why it comes so close and I don't really understand why I used this formula. Maybe someone can explain if it's just luck or there is some reason for using a square root. I'll probably be asked why this formula at the presentation.

Available trips - Total of all available trips on that day in this area.
Lowest bound - Least amount of possible trips taken (I calculated it by having a total distance of driving all available chronologically trips one by one, the pure driving time by amount of trips and add 6 minutes for each trip for loading/unloading time. 6 minutes is the average load/unload for 5000 trips last year. It gives 39 minutes. Time a car is available on that day, divided by 39 minutes gives a lowest_bound number of trips.

Overlap factor - I used excel to count the number of overlapping trips on a particular day with the idea that more trips can be taken as coloads if they happen to be available for pickup within 30 minutes of each other and 15 min driving distance from one another. In that case trip counts as 1 extra in the same time as the other.

I figured some of the overlapping trips + some of the trips not taken in lowest_bound will also be driven. I used a square root for the calculation but I can't explain why other than I've seen an equation some time ago that uses a sqrt.

It seems to me like it works.

Can anyone explain why? I'm a bit worried I'll be asked at my presentation why I chose to do that.

I appreciate your time.

 

[DaveC426913]

Can I suggest that you attach a full scale screen grab, so we can read the chart?
You don't have to embed it in the post, there's an "Attach files" option (I think it's in the lower right corner of your editor).

 

[jedishrfu]

For a limited set of data you can always find an equation that works but will usually be a mystery.

At Cornell, some researchers built a software tool called Eureqa that discovered the equations of motion for a compound pendulum and really impressed the scientific community. The equations made sense physics wise as we knew how to derive them.

Later the same software was used to find the hidden equations behind some biology data and it did which made the biologists quite happy. However they couldn’t publish their results because the couldn’t explain the equation, it just worked.

 

[Twigg]

However they couldn’t publish their results because the couldn’t explain the equation, it just worked.

Funny, when Cauchy did that he didn't just get published, he got an equation named after him (again)!

It seems to me like your goal is to calculate profits. In that case, isn't the accuracy of your predictions the most important thing? If someone asks you "why did you use this formula", what's wrong with saying "because it works"? You can track sum of residuals squared (see wikipedia) to quantify how good your formula is.

If you really want to prove that a square root is the right functional form, then I suggest you plot your experimental data vs. the "available trips" on a log-log scale. If the slope of this data is nearly 1/2 (particularly for large values of "available trips"), then the square root was good call. This is most useful when you have a large spread in the values of "available trips". This is the standard trick when you're trying to fit a power law of the form $y = Ax^B$.