Jackhammer on Vehicle Suspension, Unsprung Mass, Tire patch load

[kazx9r]

TL;DR Summary

I was curious about what would happen if you take a jack hammer on a unsprung suspension.

Hello all, I wanted to know what would happen if I put a jack hammer system on the unsprung part of the suspension, I posted this on the engineering forum but couldn't get a complete answer.
https://www.eng-tips.com/viewthread.cfm?qid=512117
Basically the argument was if the reaction would react on the chassis in the same amount of load a jackhammer impacts an object .
Taking the main points from before,

We're talking about a vehicle on a smooth surface, taking a turn, no bumps, the turn lasts less than a second or that the amount I need additional load on the inside tire is less than a second and I want to know the static force if you take a jack hammer type of machine to the unsprung part of the vehicle. I only need it for a split second while I'm either losing grip or making a turn. An illustration:

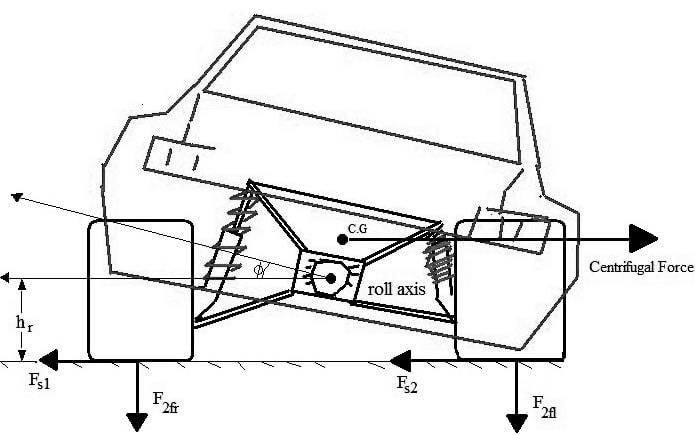Would it create any kind of load on the tire patch? And would the reaction load just act upon the chassis because obviously the jack hammer is mounted to the car (could be on the unsprung part or chassis)? How to calculate the static load of a jack hammer?

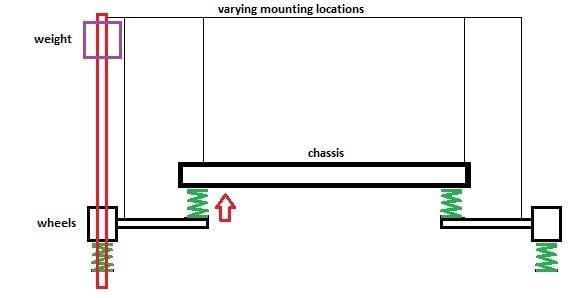
A simple experiment I ran (not sure if it's correct), I took a heavy weight and varied the location where I want to mount my so called jack hammer, basically right near the unsprung part of the suspension seemed the best.
What I noticed the rebound of only 25%, so basically the chassis moved up.

Some topics that were similar that I looked at:

https://physics.stackexchange.com/questions/175956...

"For example, if a 5 pound hammer is swung at 50 feet per second, then the kinetic energy of the hammer is 5 * 50 * 50 / 64.32 = 194 foot pounds. If this then compresses a forging by 1/8 of an inch, then neglecting rebound, then it is about 194 * 96 or about 18,600 pounds of force on average. This is because 1/8" = 1/96th of a foot, and the average force is foot pounds / feet over which the force acts."

https://www.physicsforums.com/threads/linear-impul...

"During Operation the jack hammer develops on the concrete surface develops a force @ t=0 f=0, @ t=.2, F=90, @ t=.4, F=0. Graph looks like a triangle To achieve this the 2lb spike S, is fired from rest into the surface @ 200ft/s. Determine the speed of the spike just after rebounding"

Initial velocity: 60.96 m/s
Final rebound velocity:
Return Momentum = RP RP = mv = -24.799 = .907v therefore v = -27.341 m/s

Not sure how correct the above is, but I wanted to post what I looked at, it appears the rebound has far less velocity and given what I'm asking, it should transfer less force to the chassis or does it?

A typical jack hammer from Home Depot, it has a energy rating 46.5ft-lbs, not max impact load, so how do I calculate it or come close to finding static load?

Lets say a tire compresses .25" from the impact (or .0208 ft or 1/48th of a foot), so static load is 46.5ft-lbs X 48 = 2232 lbs per blow?
Would the reaction on the chassis also be this load? or would it be less or more? If less, why is it less?

Is this the correct formula? I don't think i have enough know values to find the reaction load on the chassis, can anyone help?

Sorry for the long post.

 

[Baluncore]

The ABS system will be very confused, like driving on a corrugated road surface.

The jackhammer will destroy your wheel bearings.

The tire contact patch area will oscillate about the average. Your wheel will spin, then stick if you are lucky, then spin again.

 

[kazx9r]

Which is exactly what any other traction control system does. A lot of variables involved but more looking for where the reaction forces would end up, if the hammer is mounted to the chassis, would it put an equivalent force on the chassis, and would the recoil force be the same as the impact force?

Edit to add: We're talking about on a turn, there is no braking going on and it's most likely a track vehicle, so no abs. But good point.

 

[jack action]

but more looking for where the reaction forces would end up

Ultimately, accelerating the sprung mass up.

Forget about a jackhammer for now and imagine a hydraulic piston slowly applying a force between the sprung and unsprung masses: What happens? How different would it be if the hydraulic piston is turned on & off sequentially?

You should do a proper free body diagram.

 

[Baluncore]

A lot of variables involved but more looking for where the reaction forces would end up, if the hammer is mounted to the chassis, would it put an equivalent force on the chassis, and would the recoil force be the same as the impact force?

The hammer force would average zero. The short sharp downward impulses would lift the pneumatic wheels off the ground for most of the time.

The sprung mass (body) would be isolated from the jackhammer by the spring suspension.

The shock absorber system would be subjected to the impulses, which would "pump down" and lower the body relative to the axle and hubs.

 

[kazx9r]

Ultimately, accelerating the sprung mass up.

Forget about a jackhammer for now and imagine a hydraulic piston slowly applying a force between the sprung and unsprung masses: What happens? How different would it be if the hydraulic piston is turned on & off sequentially?

You should do a proper free body diagram.

Edit to add: yes accelerating the mass up as I stated the chassis would move up but by how much? Is the rebound velocity and force the same? The reason I posted the other link about return velocity. If rebound force is less then would we have a net gain of load downwards?That’s really the tough part, a slow moving piston has very little momentum, a free body diagram would just show equal amount of force on wherever the hammer is mounted so there would be no change in load on the vehicle.

But a fast moving hammer is a bit difficult, we need the mass of the weight of the hammer object and velocity of that hammer to find the work done, none of which I have from the Jack hammer specs.

 

[kazx9r]

The hammer force would average zero. The short sharp downward impulses would lift the pneumatic wheels off the ground for most of the time.

The sprung mass (body) would be isolated from the jackhammer by the spring suspension.

The shock absorber system would be subjected to the impulses, which would "pump down" and lower the body relative to the axle and hubs.

I agree, is this different than the 2nd link I posted where the return velocity was less than the initial velocity or are you talking about something else?

I also picture the wheel moving back up after the impulse but with far less force but you’re saying the force would be exactly the same? So if the wheel compresses 1/4” the rebound would be 1/4” plus the an additional how much?

 

[berkeman]

The ABS system will be very confused, like driving on a corrugated road surface.

The jackhammer will destroy your wheel bearings.

The tire contact patch area will oscillate about the average. Your wheel will spin, then stick if you are lucky, then spin again.

Which is exactly what any other traction control system does.

No, that's not how traction control works. Traction control modulates the drive and brakes to maximize the traction force of the tire on the road. It does not do anything actively with the suspension. (Perhaps on the latest race suspensions it may adjust the damping to try to keep the tire in maximum contact with the road, but that's passive damping modulation, not active actuation of a drive force into the suspension.)

Edit to add: We're talking about on a turn, there is no braking going on and it's most likely a track vehicle, so no abs.

Are you trying to figure out a way to improve race car traction in turns? If so, I don't think it will work. If it could, I'm pretty sure the thousands of race teams out there would have figured this out already...

Paging @Ranger Mike

 

[jrmichler]

I would solve it as follows:
1) Knowing that a typical car has a sprung natural frequency of 1 to 1.5 Hz, and unsprung natural frequency on the order of 10 Hz, calculate the spring constants and masses.
2) Simplify the free body diagram (FBD) to a quarter car model: a spring for the tire, an unsprung mass, and spring to the body, a damper, and a body mass. Many quarter car models also include a damper in parallel with spring representing the tire. Typical quarter car model:

3) If you really want to analyze a single blow jackhammer, you need the mass and velocity at impact of the mass in the jackhammer that does the hammering. That mass has a momentum and a kinetic energy at impact.
4) Since the impact is steel on steel, the impact duration is short relative to the two natural frequencies.
5) Therefore, I would start with a simplified analysis. All parts in an initial position, and the unsprung mass has an initial velocity calculated from the mass and velocity of the jackhammer mass. Fully analyze this case.
6) The next step is to add a bump in the road. Since you are interested in traction, solve the model for the tire force against the road without the jackhammer.
7) When the models in step 5 and step 6 are fully working, combine them and optimize the timing and force of the jackhammer. Model output is force between tire and road.
8) Now add in the jackhammer reaction force against the car mass, and the body response to the tire/road force.

Are you trying to figure out a way to improve race car traction in turns? If so, I don't think it will work.

Neither do I, but let the OP figure it out for himself.

I would do the entire analysis in simulation rather than trying to solve it analytically. But that's because I think like an engineer, not a physicist.

 

[kazx9r]

No, that's not how traction control works. Traction control modulates the drive and brakes to maximize the traction force of the tire on the road. It does not do anything actively with the suspension. (Perhaps on the latest race suspensions it may adjust the damping to try to keep the tire in maximum contact with the road, but that's passive damping modulation, not active actuation of a drive force into the suspension.)Are you trying to figure out a way to improve race car traction in turns? If so, I don't think it will work. If it could, I'm pretty sure the thousands of race teams out there would have figured this out already...

Paging @Ranger Mike

Exactly, I said that in my initial post, what I meant by this is how a traction control system works is that I'm looking to use it as regaining traction during loss of traction by giving it a few milliseconds of extra load.

Most race teams couldn't use this because it's considered an active suspension or electronic aids which is banned in most racing sports, this is just something I was curious about.

Lets stay on topic, this is not about would it work or wouldn't, it's about finding the loads and the formula's used for finding the loads, the two links I posted seem to use accurate formulas.

 

[kazx9r]

I would solve it as follows:
1) Knowing that a typical car has a sprung natural frequency of 1 to 1.5 Hz, and unsprung natural frequency on the order of 10 Hz, calculate the spring constants and masses.
2) Simplify the free body diagram (FBD) to a quarter car model: a spring for the tire, an unsprung mass, and spring to the body, a damper, and a body mass. Many quarter car models also include a damper in parallel with spring representing the tire. Typical quarter car model:
View attachment 332962
3) If you really want to analyze a single blow jackhammer, you need the mass and velocity at impact of the mass in the jackhammer that does the hammering. That mass has a momentum and a kinetic energy at impact.
4) Since the impact is steel on steel, the impact duration is short relative to the two natural frequencies.
5) Therefore, I would start with a simplified analysis. All parts in an initial position, and the unsprung mass has an initial velocity calculated from the mass and velocity of the jackhammer mass. Fully analyze this case.
6) The next step is to add a bump in the road. Since you are interested in traction, solve the model for the tire force against the road without the jackhammer.
7) When the models in step 5 and step 6 are fully working, combine them and optimize the timing and force of the jackhammer. Model output is force between tire and road.
8) Now add in the jackhammer reaction force against the car mass, and the body response to the tire/road force.

Neither do I, but let the OP figure it out for himself.

I would do the entire analysis in simulation rather than trying to solve it analytically. But that's because I think like an engineer, not a physicist.

Thank you, let me read this a bunch of times before I understand it a bit better, I'll never fully understand it but its helpful.

I'm guessing Kt here would be the spring constant of the tire? for this I would assume something about 1200 lbs/inch. The other variable that comes to mind is, during rebound, that itself would have some kinetic energy, assume most of the rebound would be dampened by the vehicle suspension, so if the hammer repeats the blow, the blow has to overcome the kinetic energy of the rebound and if anything is left over not including the weight on that wheel, then it would have less force, eventually it should level out to zero, is this what is meant by the force will average to zero?

 

[jack action]

With a jackhammer, the force depends not only on the jackhammer itself but on what it impacts as well.

In post #9, you have a simplified free body diagram (FBD). Between the spring and the damper, you would add your jackhammer. What you know about your jackhammer is the impact energy per blow (46.5 ft.lb/blow or 63 N.m/blow) and the blows per minute (1100 BPM or 0.0545 s/blow). With this, you have the output power $P$ of the jackhammer:
$$P = \frac{63\ N.m}{0.0545\ s} = 1156\ W$$
Since the jackhammer has a 15 A / 120 V motor, it has an input power of 15 A X 120 V = 1800 W, so this gives you an idea of the jackhammer's efficiency.

Back to your FBD, the force acting will be $F = \frac{P}{v}$ or, more precisely:
$$F_j = \frac{P}{\dot{x}_b - \dot{x}_w}$$
Note that theoretically, the force is infinite when both masses travel at the same speed. In reality, something would deform and the force would depend on the displacement. This force is added to the two other forces - the spring and the damper:
$$F_s = k_s(x_b - x_w)$$
$$F_d = C(\dot{x}_b - \dot{x}_w)$$

 

[Baluncore]

4) Since the impact is steel on steel, the impact duration is short relative to the two natural frequencies.

Note that theoretically, the force is infinite when both masses travel at the same speed. In reality, something would deform and the force would depend on the displacement.

Good jack hammers drive through two opposed pistons in a cylinder. There is no steel-on-steel contact that would spread or mushroom the steel. Instead, a Gaussian pulse is generated as one piston bounces off the other, with a thin cushion of (hot) compressed air between the two. By varying the initial air volume, a hammer can be tuned to spread the Gaussian impulse in time, to maximise energy lower down in the frequency spectrum. That eliminates irresistible infinite forces, which might be used to better protect the axle assembly and connections.

 

[kazx9r]

Thank you all