Jordan Chains to solve x'=Ax, complex-valued.

[kostoglotov]

This isn't a homework help question, I am asking about a general case as the text hasn't fleshed out it's explanation enough for me.

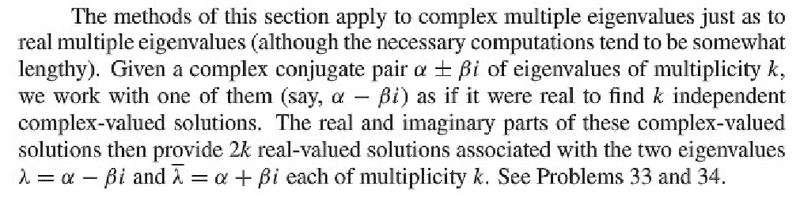
So, I've just seen how Jordan Chains can be applied to solve some applied problems involving solving x'=Ax.

My question is about what they specifically mean in this copy-pasted paragraph above.

Would they mean that, I should find a Jordan Chain of length k for lambda = alpha and then another Jordan Chain of length k for lambda = beta? And if so, what would the general form of the solution look like?

Take a three by three case with complex eigenvalue of defect 2. Would the general solution look like:

$$\lambda = \alpha, \left \{ \vec{u_1},\vec{u_2},\vec{u_3} \right \}$$
$$\lambda = \beta, \left \{ \vec{v_1},\vec{v_2},\vec{v_3} \right \}$$
$$\vec{x_1} = \vec{u_1}e^{\alpha t} \\ \vec{x_2} = (t\vec{u_1} + \vec{u_2})e^{\alpha t} \\ \vec{x_3} = \left(\frac{1}{2}t^2\vec{u_1} + t\vec{u_2}+\vec{u_3}\right)e^{\alpha t} \\ \\ \vec{x_4} = \vec{v_1}(\cos{\beta t} + \sin{\beta t}) \\ \vec{x_5} = (t\vec{v_1} + \vec{v_2})(\cos{\beta t} + \sin{\beta t}) \\ \vec{x_6} = \left(\frac{1}{2}t^2\vec{v_1} + t\vec{v_2}+\vec{v_3}\right)(\cos{\beta t} + \sin{\beta t})$$

Or

$$\vec{x_1} = \vec{u_1}e^{\alpha t}(\cos{\beta t} + \sin{\beta t}) \\ \vec{x_2} = (t\vec{u_1} + \vec{u_2})e^{\alpha t}(\cos{\beta t} + \sin{\beta t}) \\ \vec{x_3} = \left(\frac{1}{2}t^2\vec{u_1} + t\vec{u_2}+\vec{u_3}\right)e^{\alpha t}(\cos{\beta t} + \sin{\beta t}) \\ \\ \vec{x_4} = \vec{v_1}e^{\alpha t}(\cos{\beta t} + \sin{\beta t}) \\ \vec{x_5} = (t\vec{v_1} + \vec{v_2})e^{\alpha t}(\cos{\beta t} + \sin{\beta t}) \\ \vec{x_6} = \left(\frac{1}{2}t^2\vec{v_1} + t\vec{v_2}+\vec{v_3}\right)e^{\alpha t}(\cos{\beta t} + \sin{\beta t})$$

or something else?

 

[jvicens]

I can provide some clarification on Jordan chains and their application in solving systems of differential equations.

A Jordan chain is a sequence of vectors that can be used to construct a Jordan basis for a matrix. In the context of solving x'=Ax, finding a Jordan chain for a specific eigenvalue, say alpha, means finding a sequence of vectors that can be used to construct a Jordan basis for the matrix A with eigenvalue alpha.

In the case of a complex eigenvalue with defect 2, you would need to find two Jordan chains, one for the real part (alpha) and one for the imaginary part (beta). The general form of the solution would depend on the specific problem and the structure of the matrix A.

In the example you provided, it looks like you have found two Jordan chains, one for alpha and one for beta, and have used them to construct solutions for each eigenvalue. This is one possible approach, but the specific form of the solution will depend on the problem and the matrix A.

In general, the solution to a system of differential equations involving Jordan chains will have the form of a linear combination of vectors multiplied by exponential functions. The specific form of the solution will depend on the number of eigenvalues, the dimension of the matrix, and the structure of the Jordan chains.

I hope this helps clarify the concept of Jordan chains and their application in solving systems of differential equations. If you have any further questions, please feel free to ask.