MHB Katie's Question: Find f(2) & f'(2) of Tangent Line y=4x-5

[MarkFL]

Here is the question:

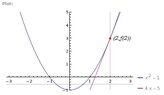
If an equation of the tangent line to the curve y=f(x) at the point where a=2 is...?


y=4x-5, find f(2) and f'(2)

Please walk me through this question step by step.

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Katie,

Consider the following diagram, showing the function $f(x)=x^2-1$ and its tangent line $y=4x-5$:

View attachment 1403

As you can see, the instantaneous slope of the function must match the slope of the tangent line at the point of tangency, and the value of the function at that point must be equal to the value of the tangent line at that point since they touch there. Hence, we must have:

$$f'(2)=\frac{d}{dx}(4x-5)=4$$

$$f(2)=y(2)=4(2)-5=3$$