MHB Katresha Davis' Trig Questions: Distance, Altitude & Ratio

[MarkFL]

Here are the questions:

Prealgebra math problems ?

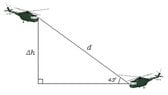
The pilot of a helicopter at an altitude of 6,000 ft sees a second helicopter is 4,000 ft. What is the distance from the first helicopter to the second along the line of sight?
6. What is the difference in altitude between the two helicopters ?
7. What trigonometric ratio will you use to find d ?
8. Substitute 43 for the angle measure and 2,000 for the opposite side
9. Multiply each side by d
10. Divide each side by sin 43 degrees
11. Use a calculator to simply

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello Katresha Davis,

Please refer to the following diagram:

View attachment 1228

6.) We may find the difference in altitude between the two helicopters by subtracting the altitude of the lower helicopter from the altitude of the higher helicopter:

$$\Delta h=(6000-4000)\text{ ft}=2000\text{ ft}$$

7.) We know the side opposite the given angle, and we are wanting to find the hypotenuse, so we should use the sine function as it relates an angle, the side opposite the angle and the hypotenuse:

$$\sin(\theta)=\frac{\text{opposite}}{\text{hypotenuse}}$$

8.) Using the values in our problem, we may state:

$$\sin\left(43^{\circ} \right)=\frac{2000}{d}$$

9.) Multiplying both sides by $d$, we obtain:

$$d\sin\left(43^{\circ} \right)=2000$$

10.) Dividing both sides by $\sin\left(43^{\circ} \right)$, we get:

$$d=\frac{2000}{\sin\left(43^{\circ} \right)}$$

11.) Using a calculator, we find:

$$d\approx2932.55837127925\text{ ft}$$