- 3,800
- 1,856
In September 1963, Roy Kerr described the geometry of uncharged rotating black holes (ie, Kerr Black Holes). This Kerr geometry included (or was presumed to include) a feature called a ring singularity.
But after apparently staring at the blackboard for 60 years, Roy just got up and drew a large and emphatic question mark over that ring singularity thing.
In a 20 page article published on ResearchGate, Roy states:
Just to be clear, I have not made any serious attempt to follow the math in Kerr's new paper.
I have read the "Cliff's Notes" equivalent (am I dating myself?) here: "Big Think" article.
But I need to provide some cautions about that "Big Think" article: It provides much lighter reading, but it also includes material that goes beyond Kerr's paper. For example, the Big Think article includes this revised Penrose Diagram:
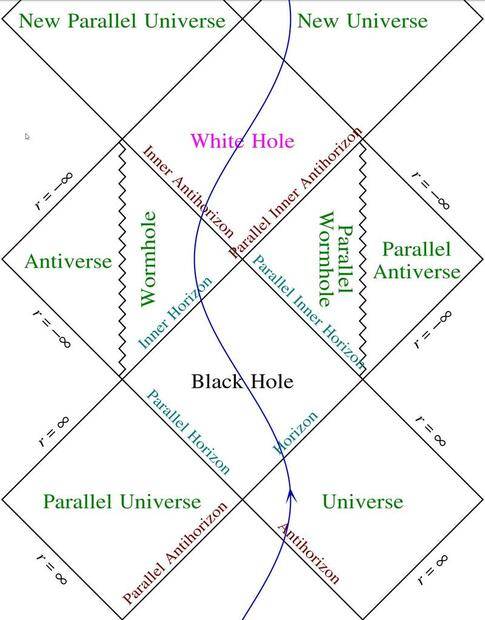
This diagram is not described or referenced in Kerr's article. Nor does Kerr's article mention worm holes.
The first thing I noticed with that diagram is the missing "You are Here" tag. And If you ever wondered how to visit the interior of a Black Hole and live to tell about it, then place that "you are here" tag in the "New Universe". Then you can wonder what will become of all this "new matter" coming into your "New Universe" once Hawking Radiation evaporates the Black Hole in the "Universe" that it was borrowed from.
But after apparently staring at the blackboard for 60 years, Roy just got up and drew a large and emphatic question mark over that ring singularity thing.
In a 20 page article published on ResearchGate, Roy states:
So, Roy will let you slide on that FALL thing, but if you want to claim a singularity it's time to show the proof.The consensus view for sixty years has been that all black holes have singularities. There is no direct proof of this, only the papers by Penrose outlining a proof that all Einstein spaces containing a ”trapped surface” automatically contain FALL’s [finite affine length light]. This is almost certainly true, even if the proof is marginal. It was then decreed, without proof, that these must end in actual points where the metric is singular in some unspecified way. Nobody has constructed any reason, let alone proof for this. The singularity believers need to show why it is true, not just quote the Penrose assumption.
Just to be clear, I have not made any serious attempt to follow the math in Kerr's new paper.
I have read the "Cliff's Notes" equivalent (am I dating myself?) here: "Big Think" article.
But I need to provide some cautions about that "Big Think" article: It provides much lighter reading, but it also includes material that goes beyond Kerr's paper. For example, the Big Think article includes this revised Penrose Diagram:
This diagram is not described or referenced in Kerr's article. Nor does Kerr's article mention worm holes.
The first thing I noticed with that diagram is the missing "You are Here" tag. And If you ever wondered how to visit the interior of a Black Hole and live to tell about it, then place that "you are here" tag in the "New Universe". Then you can wonder what will become of all this "new matter" coming into your "New Universe" once Hawking Radiation evaporates the Black Hole in the "Universe" that it was borrowed from.