- #1
JaWiB
- 283
- 0
This is my first post, so I apologize if any formatting is off or if I'm not clear enough.
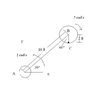
A ride in an amusement park consists of a rotating arm AB having a constant angular velocity \omega_{AB}=2rad/s about point A and a car mounted at the end of the arm which has a constant angular velocity \omega'={-.5k}rad/s, measured relative to the arm. At the instant shown, determine the velocity and acceleration of the passenger at C.
Since I don't have a scanner handy, I'm attaching my paint replication of the figure.
For now, I'm just looking at solving for velocity, and I think I'll be able to find acceleration if I can figure that part out.
I'm using the kinematic equations derived in the book for a rotating and translating reference frame x,y. Using the point B in the figure as the origin for these axes, and the point A in the figure for a fixed reference frame X,Y, we have:
\vec{V_{C}} = \vec{V_{B}} + \vec{\omega_{BC}}\times\vec{r_{C/B}}+(\vec{V_{C/B}})_{xy}
This didn't seem too complicated to me, but I can't get the same answer that the book does. First of all, I think that the (\vec{V_{C/B}})_{xy} term should be zero since C is fixed to B (it's not moving with respect to the x,y axes).
\vec{V_{B}} should be equal to the angular velocity of the AB arm crossed with it's radius (2 rad/s * 10 ft tangent to the arm) which ends up as { -20icos(60) + 20jsin(60) } ft/s = { -10i + 10\sqrt{3}j } ft/s
Then {\omega_{BC}}\times\vec{r_{C/B}} is completely in the negative X direction at .5 rad/s * 2 ft which is just { -1i } ft/s
Finally, my answer is the sum of those two vectors: { -11i + 10\sqrt{3}j } ft/s
The answer the book gives, however, is { -7i + 17.3j } ft/s. So the Y component of my answer is correct, but somehow my X component's magnitude is too great. What am I missing?
Hopefully my figure is clear enough. C is attached 2ft from the center of the clockwise rotating disk B, which is in turn attached to a 10ft arm which is rotating anti-clockwise about A. The X and Y axes given are horizontal and vertical.
Homework Statement
A ride in an amusement park consists of a rotating arm AB having a constant angular velocity \omega_{AB}=2rad/s about point A and a car mounted at the end of the arm which has a constant angular velocity \omega'={-.5k}rad/s, measured relative to the arm. At the instant shown, determine the velocity and acceleration of the passenger at C.
Since I don't have a scanner handy, I'm attaching my paint replication of the figure.
For now, I'm just looking at solving for velocity, and I think I'll be able to find acceleration if I can figure that part out.
Homework Equations
I'm using the kinematic equations derived in the book for a rotating and translating reference frame x,y. Using the point B in the figure as the origin for these axes, and the point A in the figure for a fixed reference frame X,Y, we have:
\vec{V_{C}} = \vec{V_{B}} + \vec{\omega_{BC}}\times\vec{r_{C/B}}+(\vec{V_{C/B}})_{xy}
The Attempt at a Solution
This didn't seem too complicated to me, but I can't get the same answer that the book does. First of all, I think that the (\vec{V_{C/B}})_{xy} term should be zero since C is fixed to B (it's not moving with respect to the x,y axes).
\vec{V_{B}} should be equal to the angular velocity of the AB arm crossed with it's radius (2 rad/s * 10 ft tangent to the arm) which ends up as { -20icos(60) + 20jsin(60) } ft/s = { -10i + 10\sqrt{3}j } ft/s
Then {\omega_{BC}}\times\vec{r_{C/B}} is completely in the negative X direction at .5 rad/s * 2 ft which is just { -1i } ft/s
Finally, my answer is the sum of those two vectors: { -11i + 10\sqrt{3}j } ft/s
The answer the book gives, however, is { -7i + 17.3j } ft/s. So the Y component of my answer is correct, but somehow my X component's magnitude is too great. What am I missing?
Hopefully my figure is clear enough. C is attached 2ft from the center of the clockwise rotating disk B, which is in turn attached to a 10ft arm which is rotating anti-clockwise about A. The X and Y axes given are horizontal and vertical.
Attachments
Last edited:
