Kinematics of a Pendulum with Two Different Masses

[Kokobird321]

Summary:: Classical problem about a pendulum!

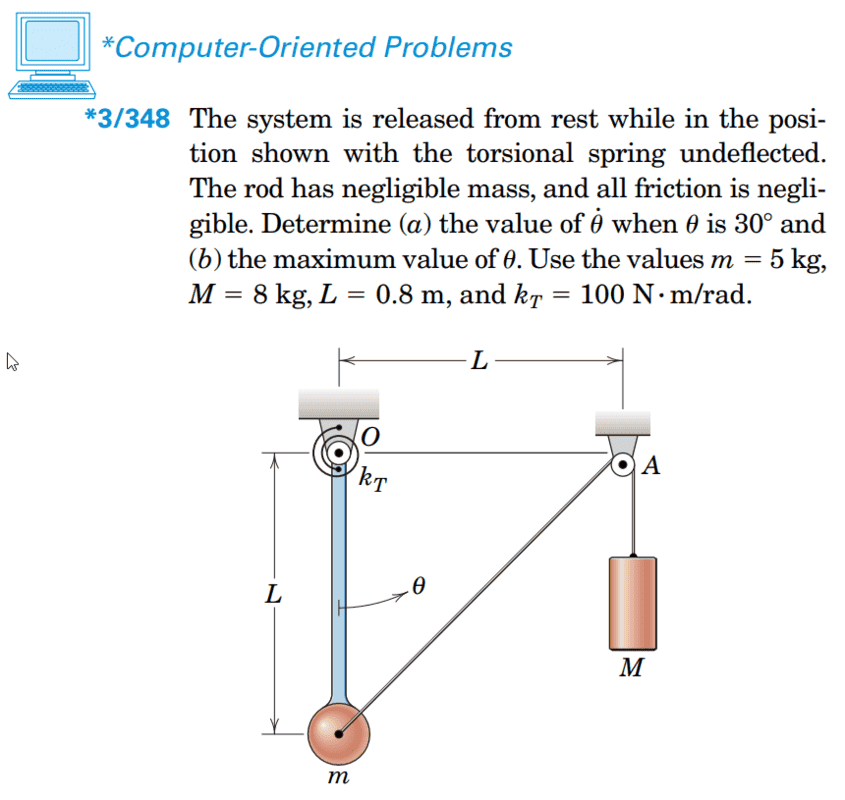
The problem itself:

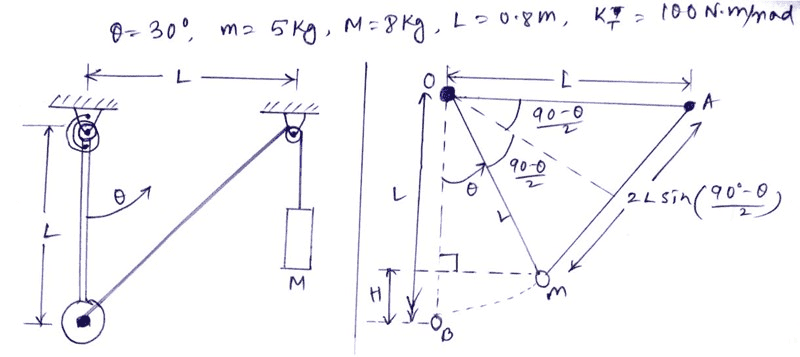
My FBD:

I want to solve the problem with vectors, I think that you can use energy principle somehow. If we define the vector $\vec{O}_B=\begin{bmatrix}0\\ -1\end{bmatrix}$ and define a rotational matrix where

$$R=\begin{bmatrix}cos\varphi & -\sin\varphi\\ \sin\varphi & \cos\varphi\end{bmatrix}$$

just to rotate the vector $O_B$ 30 degrees counterclockwise, but I will need to know its velocity $\dot{\theta}$ when $\theta=30^{\circ}$ somehow. Not sure how to proceed though.

 

[kuruman]

I think mechanical energy conservation is the way to go. Start with total mechanical energy equal to zero and then sort out the various kinetic and potential energies when the angle is 30^o.

 

[Kokobird321]

It becomes very trivial, I wanted a different approach

 

[kuruman]

It becomes very trivial, I wanted a different approach

Lagrangian formulation? I am not sure whether the equations of motion are solvable analytically.

 

[Kokobird321]

Sure why not! For the lagrangian I get

$$\mathcal{L}=T-V=\frac{1}{2}m(L\dot{\theta})^2+\frac{1}{2}M(L\dot{\theta})^2+\frac{1}{2}k_T\theta^2-(Mgh-mgH)$$

so

$$\mathcal{L}=T-V=\frac{1}{2}m(L\dot{\theta})^2+\frac{1}{2}M(L\dot{\theta})^2+\frac{1}{2}k_T\theta^2-Mg\left[\sqrt{2}L-2Lsin\left(\frac{90-\theta}{2}\right)\right]+mg\left[L-L\cos\theta\right]$$

$$\frac{\partial\mathcal{L}}{\partial\theta}=k_T\theta-MgL\frac{1}{2}\cos\left(45-\frac{\theta}{2}\right)+mgL\sin\theta$$

and

$$\frac{\partial\mathcal{L}}{\partial \dot{\theta}}=mL^2\dot{\theta}+ML^2\dot{\theta}\Longrightarrow\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{\theta}}\right)=mL^2\ddot{\theta}+ML^2\ddot{\theta}=\ddot{\theta}(mL^2+ML^2).$$

Euler-Lagrange gives

$$\frac{d}{dt}\left(\frac{\partial\mathcal{L}}{\partial\dot{\theta}}\right)=\frac{\partial\mathcal{L}}{\partial\theta}\iff \ddot{\theta}(mL^2+ML^2)=k_T\theta-MgL\frac{1}{2}\cos\left(45-\frac{\theta}{2}\right)+mgL\sin\theta$$

$$\ddot{\theta}=\frac{1}{mL^2+ML^2}\left[k_T\theta-MgL\frac{1}{2}\cos\left(45-\frac{\theta}{2}\right)+mgL\sin\theta\right]$$

How do I proceed from here?

 

[kuruman]

What are your generalized coordinates? What are the constraints?

The term $\dfrac{1}{2}ML^2\dot \theta^2$ doesn't look right to me for the kinetic energy of the vertically hanging mass.