Kinematics of mass on a semi-circular slide

[oddjobmj]

Homework Statement

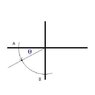
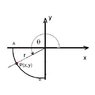
A mass slides down a segment of a circle starting from rest at A. It has a radius of R. Find the speed of the mass at the bottom ignoring friction. Also, find the time for the ice cube to go from A to B.

As far as solving for the time I am told not to calculate the integral but plot the function and estimate the area below the curve.

I attached an image of the diagram I am provided.

Homework Equations

U=mgr
K=.5mv²

T=$\frac{2πr}{v}$

The Attempt at a Solution

I believe the first part is simple. I can use the conservation of energy to find v because I know that at A there is no kinetic energy, it is all potential. The opposite is true at B.

.5mv²=mgr

.5v²=gr

v_f=$\sqrt{2gr}$

What I am having trouble doing, because it has been a while since the section on circular motion , is relating v and t. v in the form I have expressed it (v_f) is a constant so it doesn't really help me find t.

Any suggestions on a next step? Thanks!

 

[haruspex]

you just need to generalise what you did to the case where it has not yet reached B. Suppose it has traversed an angle theta of the arc. What is the speed there?

 

[oddjobmj]

Ah, yes. Thank you!

.5mv₀²+mgr=.5mv²+mg(r-??)

In the case of the potential energy h happens to equal r initially but as it moves the height changes. To simplify this we can look at the y-axis exclusively. y(t)=rcos(θ)

I realize, usually, y(t)=rsin(theta) but we want y(t) to equal r at the start, where theta=π, else we would be starting with no potential and ending with no velocity.

So perhaps:

.5mv₀²+mgr=.5mv²+mgrcos(θ)

At no point is the constant v₀ not zero so we can ignore that segment:

mgr=.5mv²+mgrcos(θ)

v=$\sqrt{2gr(1-sin(θ))}$

This checks out at the final conditions where θ=$\frac{3π}{2}$

I'm not sure how to represent theta as a function of time, though. My understanding is that I want to be able to write t=something. Theta and v are both functions of time, I realize. Would it be useful to use the T=2πr/v relationship here? Making T=t?

 

[haruspex]

v=$\sqrt{2gr(1-sin(θ))}$

This checks out at the final conditions where θ=$\frac{3π}{2}$

I'm not sure how to represent theta as a function of time, though. My understanding is that I want to be able to write t=something.

What is the relationship between v and $\dot \theta$?

 

[oddjobmj]

t=θr/v

θ=tv/r

$\dot{θ}$=v/r

 

[haruspex]

$\dot{θ}$=$\frac{v}{r}$

This relationship does not look familiar to me

Perhaps more familiar as v = rω?

edit: Eh, that can't be right. Theta would be constant if the velocity were constant which doesn't make any sense.

No, v constant would make $\dot \theta$ constant. Where's the problem?

 

[oddjobmj]

Ah, yes, of course, thank you. Not sure why I was thinking about theta instead of its derivative.

Not sure how to evaluate this:

dθ/dt=$\frac{sqrt(2gr(1-cos(θ)))}{r}$

edit:

I guess if I solve for theta before plugging my value for v in I get:

dθ/dt=v/r

dθ=vdt/r

θ=vt/r+C

When t=0, θ=π, so C=π

θ=vt/r+π

t=(r/v)(θ-π)

t=$\frac{r(θ-π)}{sqrt(2grcos(θ))}$

Why is this not correct?

 

[haruspex]

t=$\frac{r(θ-π)}{sqrt(2gr(1-cos(θ)))}$

Why is this not correct?

I didn't check this properly before:

.5mv₀²+mgr=.5mv²+mgrcos(θ)

If theta is the angle traversed from the top of the arc, shouldn't that be
.5mv₀²+mgr=.5mv²+mgr(1-cos(θ))?

 

[oddjobmj]

edit: Actually, I think I mixed something up. That would mean that at t=0 we're moving and at B v=0. That's definitely not right.

At pi, t=0. So, perhaps that term is mgr(1-sin(theta)). That way when t=0, theta=pi. Since sin(pi)=0 that term will be mgr which is what we want.

That means v=sqrt(2grsin(theta))

When theta=3pi/2 v will have an imaginary part.

 

[haruspex]

At pi, t=0. So, perhaps that term is mgr(1-sin(theta)).

Sorry, yes - that's what I meant to write.

 

[ehild]

If you choose θ as shown in the figure changing from zero to pi/2, and initially both KE and PE zero,

1/2 mv^2-mgrsinθ=0.

ehild

 

[oddjobmj]

I guess I'm just not sure of the best course of action from here.

I found dθ/dt but I don't know what good that does me unless I go backwards to solve for theta and use that in my equation for v. I could represent v as dx/dt then:

dx=$\sqrt{2grsinθ}$dt

Then I could plug in my new representation of θ:

dx=$\sqrt{2grsin(vt/r+π)}$dt

Then integrating both sides I'd get 'x' which I'm not sure what that would even be in this context. I guess it would be the position on the circle so we would want to find t when the point has moved 1/4 the way around the circle or x=(.25)2πr=.5πr

This is, perhaps, the nasty integral that I am supposed to approximate the solution to.

 

[ehild]

What is x? v is the speed, and v=r dθ/dt. So $r dθ/dt = \sqrt{2grsinθ}$.
The integral can not be written in closed form, but Wolframalpha would do it for you.

ehild

 

[oddjobmj]

What is x? v is the speed, and v=r dθ/dt. So $r dθ/dt = \sqrt{2grsinθ}$.
The integral can not be written in closed form, but Wolframalpha would do it for you.

ehild

Ah, well said, thank you.

The initial problem says I will come across an integral I can not evaluate and not to use wolfram alpha to evaluate it, haha. I am supposed to plot the function and estimate the value under the curve. I'm just happy I found a nasty integral which seems to be a reasonable checkpoint.

$dθ/dt=\frac{\sqrt{2grsinθ}}{r}$

Honestly I'm not even sure of what function to plot. Beyond that, no values are given so the estimate will end up being a function of r. If I plug in g and a hypothetical r and plot:

$y=\frac{\sqrt{2grsinθ}}{r}$

y just being a placeholder variable

Should I be replacing theta with it's equivalent function of t? I'm not getting a useful plot.

 

[ehild]

You can choose r=1, and plot y=dt/dθ=(√(2g)√(sin(θ))^-1, in terms of theta in radians. Then estimate the area under the curve.


ehild

edit: thanks for the thanks, is not two too many?

 

[oddjobmj]

Thanks again, ehild.

Perhaps my format is incorrect but this is what I'm getting:

http://www.wolframalpha.com/input/?i=y=(sqrt(2*9.8*sin(theta)))^(-1),+theta=pi..3*pi/2

I actually couldn't get a plot to appear at all in mathematica.

edit: It is the least I can do in return for you help. I greatly appreciate your advice. It truly has a significant impact.

 

[ehild]

If your theta is between pi and 3pi/2 then sin(theta) is negative, and its square root is complex. The change of PE is mgsin(θ) then, and you need a minus in front of sinθ under the square root.

The formula for dθ/dt refers to the setup I have shown in my post#11, where theta goes from zero to pi/2. I plotted it out for r=1 from (almost) zero to pi/2, and integrated. The scale on the horizontal (theta) axis is in radians and the vertical axis is dt/dθ in second/radian-s.ehild

 

[oddjobmj]

Ah, thank you.

So you are saying that an easy way to get rid of the imaginary part is to leave the sin factor positive and plot between 0 and pi/2 instead of a negative sin and between pi and 3pi/2? I did finally work out the issue with my plot. The graph turned out similar to yours after I set the value inside the square root to negative.

Also, I guess once I do end up with an estimated area under the curve I could just give the answer in terms of r by multiplying the variable r by the area, correct?

Lastly, I still don't understand why this form works for the estimation. dt/dθ is basically ω(t)^-1. What is this plot representing? I'm sure I could get the answer correct at this point but I really want to make sense of it before moving on.

edit: Also, between pi and 3pi/2 sin(theta) is not negative. To make it negative under the square root I have to set the energy equation to this:

mgr=-.5v²m+mgr$\sqrt{1-sin(θ)}$ (note the tiny negative next to the kinetic energy component)

That is not correct, though. The initial potential should equal the sum of the potential and kinetic at a later point; not the difference. I'm just a bit confused about how to work the negative into a proper conservation of energy equation and why it needs to be negative.

 

[ehild]

Ah, thank you.

So you are saying that an easy way to get rid of the imaginary part is to leave the sin factor positive and plot between 0 and pi/2 instead of a negative sin and between pi and 3pi/2? I did finally work out the issue with my plot. The graph turned out similar to yours after I set the value inside the square root to negative.

Yes, it was what I suggested.

edit: Also, between pi and 3pi/2 sin(theta) is not negative.

Well, what is sin (3pi/2) (sine of 270 degree)? or sin(4pi/3)? Do you remember the unit circle representation of the trigonometric functions? In which quadrants is sinθ negative?

To make it negative under the square root I have to set the energy equation to this:
$mgr=-.5v^2 m+mgr \sqrt{1-sin(θ)}$
(note the tiny negative next to the kinetic energy component).

That is not correct, though. The initial potential should equal the sum of the potential and kinetic at a later point; not the difference. I'm just a bit confused about how to work the negative into a proper conservation of energy equation and why it needs to be negative.

You are right, it is wrong. If you count theta from the positive x-axis as shown in the attached figure, the position of the mass at P is x=rcosθ , y=rsinθ.

Both cosθ and sinθ are negative, as P is in the third quadrant. When θ increases, y gets more negative and the potential decreases as the mass moves downward. If you take the potential energy equal to mgr at point A than it is

$U=mg(r+y) = mgr(1+sinθ)$

at point P and zero at point B.

Conservation of energy means that

$1/2 mv^2+mgr(1+\sin\theta)=mgr$

Rearranging the equation, mgr cancels and you get $1/2 mv^2+mgr\sin\theta=0$

Isolate v: $v=\sqrt{-2gr\sin\theta}$, when θ changes from pi to 3pi/2.

Also, I guess once I do end up with an estimated area under the curve I could just give the answer in terms of r by multiplying the variable r by the area, correct?

Lastly, I still don't understand why this form works for the estimation. dt/dθ is basically ω(t)^-1. What is this plot representing? I'm sure I could get the answer correct at this point but I really want to make sense of it before moving on.

v is the speed and v= rω=rdθ/dt. So $d\theta /dt = \sqrt{-\frac{2g}{r}\sin\theta}$

θ(t) is function of the elapsed time, t. It is monotonous function in the range where pi≤θ≤3pi/2. The inverse function t(θ) exists in that interval and its derivative is dt/dθ, the reciprocal of the derivative of θ(t).

$$dt / d\theta = \frac{1}{\sqrt{-\frac{2g}{r}\sin\theta}}$$

The integral of dt/dθ from pi to 3pi/2 gives the elapsed time when the mass moves from point A to B. The area under the plot t(θ) between pi and 3pi/2 gives the elapsed time.

Note that r is under the square root. You can rearrange the equation to see how the time depends on r:

$$dt / d\theta = \frac{\sqrt{r}}{\sqrt{-2g\sin\theta}}$$

ehild

 

[oddjobmj]

Well, what is sin (3pi/2) (sine of 270 degree)? or sin(4pi/3)? Do you remember the unit circle representation of the trigonometric functions? In which quadrants is sinθ negative?

I have no idea what I was thinking. *facepalm* That all makes so much more sense now. I appreciate your thorough response.


I suppose then that t=$\frac{sqrt(r)}{area}$ if I plot assuming r=1? That would make sense because r is constant with respect to what would otherwise be integration.

Edit:

t≈$\sqrt{r}$/.483

 

[ehild]

I suppose then that t=$\frac{sqrt(r)}{area}$ if I plot assuming r=1? That would make sense because r is constant with respect to what would otherwise be integration.

Edit:

t≈$\sqrt{r}$/.483

No , $t=\sqrt{r} (area)$. And "area" is that below the graph of $\frac{1}{\sqrt{-2g\sin\theta}}$.

ehild

 

[oddjobmj]

Ah dang, my estimate is way off then. I'm getting the area is about .483 but using mathematica's NIntegrate I get 1.835.

 

[ehild]

The previous value you got was not accurate enough, but it had sense as an estimate.I used 1000 points to draw the curve. I do not know what Mathematica did. But you can not use Mathematica for the integration.
Just plot out the function and do the "integration" by counting the "tiles" under the curve . (Or cheat and use Wolframalpha to check yourself) The graphical integration is difficult as the function tends to infinity at the lover bound.

Spoiler

I got abut 0.58 for the area.

ehild

 

[oddjobmj]

Well, I am definitely going to stick with an estimate but I thought using mathematica to do the integral would be a good check to make sure I am not off by an order of magnitude or more. I did integrate within the given boundaries.

I also used mathematica to make the plot. I then split the graph into about 10 segments and figured the area of each little rectangle then added them up. I believe my problem is that once I got to the smaller values I estimated the remainder as 1 which is probably really low. If I use 2 there I get an answer much closer to yours.

I guess that is close enough :) I think it would be obvious if I artificially increased my estimate because these methods of estimation deal with those tendencies towards infinity rather poorly. Thanks again for all your help, ehild!