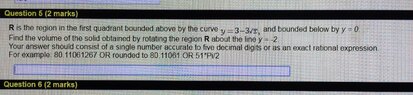
- #1
Prove It
Gold Member
MHB
- 1,465
- 24
View attachment 5626
Here is a sketch of the region R and the line to be rotated around.
View attachment 5627
Clearly the x-intercept of $\displaystyle \begin{align*} y = 3 - 3\,\sqrt{x} \end{align*}$ is (1, 0) so the terminals of the integral will be $\displaystyle \begin{align*} 0 \leq x \leq 1 \end{align*}$.
We should note that the volume will be exactly the same if everything is moved up by 2 units, with the advantage of being rotated around the x-axis.
So we want to get the volume of the solid formed by rotating $\displaystyle \begin{align*} y = 5 - 3\,\sqrt{x} \end{align*}$ around the x-axis and then subtract the volume of the solid formed by rotating $\displaystyle \begin{align*} y = 2 \end{align*}$ around the x-axis. So the volume we want is
$\displaystyle \begin{align*} V &= \int_0^1{ \pi\,\left( 5 - 3\,\sqrt{x} \right) ^2 \,\mathrm{d}x } - \int_0^1{ \pi\,\left( 2 \right) ^2 \,\mathrm{d}x } \\ &= \pi\int_0^1{ \left[ \left( 5 - 3\,\sqrt{x} \right) ^2 - 2^2 \right] \,\mathrm{d}x } \\ &= \pi\int_0^1{ \left( 25 - 30\,\sqrt{x} + 9\,x - 4 \right) \,\mathrm{d}x } \\ &= \pi\int_0^1{ \left( 21 - 30\,x^{\frac{1}{2}} + 9\,x \right) \,\mathrm{d}x } \\ &= \pi\,\left[ 21\,x - \frac{30\,x^{\frac{3}{2}}}{\frac{3}{2}} + \frac{9\,x^2}{2} \right] _0^1 \\ &= \pi\,\left[ 21\,x - 20\,x^{\frac{3}{2}} + \frac{9\,x^2}{2} \right] _0^1 \\ &= \pi\,\left\{ \left[ 21 \,\left( 1 \right) - 20\,\left( 1 \right) ^{ \frac{3}{2}} + \frac{9\,\left( 1 \right) ^2}{2} \right] - \left[ 21\,\left( 0 \right) - 20 \,\left( 0 \right) ^{\frac{3}{2}} + \frac{9\,\left( 0 \right) ^2 }{2} \right] \right\} \\ &= \pi \,\left( 21 - 20 + \frac{9}{2} - 0 \right) \\ &= \frac{11\,\pi}{2}\,\textrm{units}^3 \end{align*}$
Here is a sketch of the region R and the line to be rotated around.
View attachment 5627
Clearly the x-intercept of $\displaystyle \begin{align*} y = 3 - 3\,\sqrt{x} \end{align*}$ is (1, 0) so the terminals of the integral will be $\displaystyle \begin{align*} 0 \leq x \leq 1 \end{align*}$.
We should note that the volume will be exactly the same if everything is moved up by 2 units, with the advantage of being rotated around the x-axis.
So we want to get the volume of the solid formed by rotating $\displaystyle \begin{align*} y = 5 - 3\,\sqrt{x} \end{align*}$ around the x-axis and then subtract the volume of the solid formed by rotating $\displaystyle \begin{align*} y = 2 \end{align*}$ around the x-axis. So the volume we want is
$\displaystyle \begin{align*} V &= \int_0^1{ \pi\,\left( 5 - 3\,\sqrt{x} \right) ^2 \,\mathrm{d}x } - \int_0^1{ \pi\,\left( 2 \right) ^2 \,\mathrm{d}x } \\ &= \pi\int_0^1{ \left[ \left( 5 - 3\,\sqrt{x} \right) ^2 - 2^2 \right] \,\mathrm{d}x } \\ &= \pi\int_0^1{ \left( 25 - 30\,\sqrt{x} + 9\,x - 4 \right) \,\mathrm{d}x } \\ &= \pi\int_0^1{ \left( 21 - 30\,x^{\frac{1}{2}} + 9\,x \right) \,\mathrm{d}x } \\ &= \pi\,\left[ 21\,x - \frac{30\,x^{\frac{3}{2}}}{\frac{3}{2}} + \frac{9\,x^2}{2} \right] _0^1 \\ &= \pi\,\left[ 21\,x - 20\,x^{\frac{3}{2}} + \frac{9\,x^2}{2} \right] _0^1 \\ &= \pi\,\left\{ \left[ 21 \,\left( 1 \right) - 20\,\left( 1 \right) ^{ \frac{3}{2}} + \frac{9\,\left( 1 \right) ^2}{2} \right] - \left[ 21\,\left( 0 \right) - 20 \,\left( 0 \right) ^{\frac{3}{2}} + \frac{9\,\left( 0 \right) ^2 }{2} \right] \right\} \\ &= \pi \,\left( 21 - 20 + \frac{9}{2} - 0 \right) \\ &= \frac{11\,\pi}{2}\,\textrm{units}^3 \end{align*}$