Klein paradox in the massless case

Click For Summary
SUMMARY

The discussion centers on the Klein paradox in the massless case, particularly at the limit where the energy of the particle equals the potential step height (##E_0 = V_0##). The wave function becomes constant (##k=0##), leading to the Dirac equation yielding trivial results (##0 = 0##) for the spinor components ##\Psi_1## and ##\Psi_2##. The user concludes that, due to the continuity of the transmission coefficient ##T(E)##, the transmission coefficient remains ##T=1## even in this limit, suggesting that an electron must pass through a potential barrier without changing its group velocity.

PREREQUISITES
  • Understanding of the Klein paradox and its implications in quantum mechanics.
  • Familiarity with the Dirac equation and its application to spinor components.
  • Knowledge of wave functions and their behavior at potential steps.
  • Concept of transmission and reflection coefficients in quantum mechanics.
NEXT STEPS
  • Research the implications of the Klein paradox in various potential scenarios.
  • Study the behavior of wave functions at potential barriers and wells.
  • Explore advanced topics in quantum mechanics, such as quantum tunneling and group velocity.
  • Examine the mathematical derivation of the Dirac equation and its solutions in different contexts.
USEFUL FOR

Quantum physicists, graduate students in theoretical physics, and researchers exploring quantum mechanics and relativistic effects in particle behavior.

Paul159
Messages
15
Reaction score
4
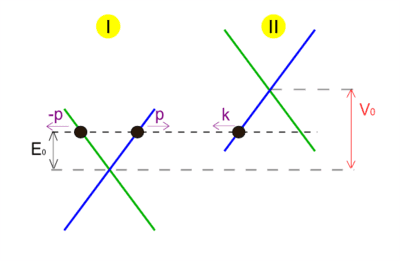
I have a question about the Klein paradox in the massless case, for a potential step of height ##V_0## (this is exactly the situation described by Wikipedia). I don't have a problem to understand the "paradox", and I think the Wikipedia's illustration is quite telling.
My question is : what append at the limit case ##E_0 = V_0## ? The "wave function" after the step is constant (##k=0##), and the Dirac equation for the spinor's components ##\Psi_1##, ##\Psi_2## become ##0 = 0##... Thus there are no conditions for the value of those components. If I choose ##\Psi_1 = \Psi_2 = 1## for example, I still get ##T=1##. If I choose ##\Psi_1 = -\Psi_2 = 1##, I get ##R=1##. I "understand" this with the fact that at the node the group velocity is not defined.
So what would really happen in real life ?

400px-Dispersion1.png
 
Physics news on Phys.org
Edit : By continuity of ##T(E)## I would say that the good answer is ##T=1##. Also if I end the step potential (I take a potential barrier), the electron coming from the left has to pass the barrier, as it can't change its group velocity. So for me ##T## is always ##1##, even in the pathological case ##E=V_0##.
 

Similar threads

Graduate Potential step at a Barrier in Quantum mechanics
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad How Is the Matrix V Related to Dirac Spinors and Tensor Products?
  • · Replies 12 ·
Replies
12
Views
2K
Graduate Ballentine on the "multicomponent state function"
  • · Replies 1 ·
Replies
1
Views
2K
Graduate Weyl Fermion in an infinite well
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Physical interpretation of phase in solutions to Schrodinger's Eqn?
  • · Replies 12 ·
Replies
12
Views
5K
Graduate Massless fermions Klein tunneling
  • · Replies 11 ·
Replies
11
Views
2K
Undergrad What do the psi_3 and psi_4 components of the Dirac equation represent?
  • · Replies 8 ·
Replies
8
Views
3K
Graduate Adjoint representation and spinor field valued in the Lie algebra
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Wilson-Sommerfeld quantization to solve square-well potential
  • · Replies 5 ·
Replies
5
Views
2K
Graduate Question about factoring the Klein-Gordon equation
  • · Replies 6 ·
Replies
6
Views
2K