Kronecker function products - matrix format

[hermish]

Hi all,
Firstly, I am not sure whether this is the area of the forum to ask this.
I have been learning and researching a completely different topic, and from this I have come across a completely new concept of the Kronecker function. I have done a google search on this to get the intro and general background of how this function works. However, there is a particular problem which I cannot put my seem to get my head around.

I have included the relevant equations below. I understand these equations EXCEPT for the Kronecker terms.

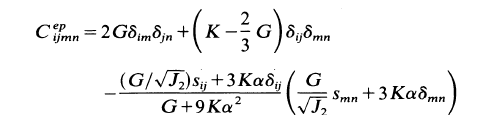
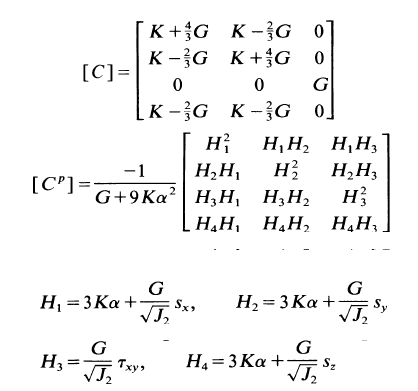
From my understanding, the Cijkl equation can be expanded to obtain the C and C^p matrices. I do not fully understand how this process works, because I do not understand how to utilise the Kronecker function.

In this context, I am guessing the i and j in the Kronecker terms represent the entry of the matrix, i.e if i=2, j=1, that means you are looking at the 2nd row and 1st column. And hence, you can go from there to calculate the term that goes into the particular matrix entry.

What I do not understand are the "m" and "n" terms. What are they? What purpose do they serve? Can I just set any number for "m" and "n"

Thanks in advanced for the help.

 

[davidmoore63@y]

The Kronecker symbol delta(i,j) means 1 if i=j and 0 otherwise. If you are working in 3 dimensions then the matrix delta(i,j) is the identity matrix consisting of 1s on the diagonal and zeroes elsewhere.

m and n are free indices. What may be going on is a summation over these indices, hence they disappear and you only have i and j left, so the "contracted" C has only 2 free indices and may be written down as a matrix. Just a guess.

 

[hermish]

The Kronecker symbol delta(i,j) means 1 if i=j and 0 otherwise. If you are working in 3 dimensions then the matrix delta(i,j) is the identity matrix consisting of 1s on the diagonal and zeroes elsewhere.

m and n are free indices. What may be going on is a summation over these indices, hence they disappear and you only have i and j left, so the "contracted" C has only 2 free indices and may be written down as a matrix. Just a guess.

Hi
Thanks very much for the response

You have also reminded me about this whole notion of 3 dimensions and 1s sitting on the diagonal that is not sitting well with me. Firstly, in all honesty, I am not even sure whether this whole thing is regarded as 3 dimension or whatever number of dimensions. There doesn't seem to be anything in the equation that suggests we are working in 3 dimensions. Regardless of that, whether it's 3 dimensions, 2 dimensions, 4 dimensions or whatever, the typical format of the Kronecker function is a 3x3 matrix (this appears on every site on google search), in the case here it contains 4 x 3 matrices which are obviously not compatible. However, I am guessing that since a couple of zeroes appear in the third row and third column, this may have something to do with making it compatible with a 3x3 matrix?

Finally, I cannot seem to gather what you mean by a "summation over these indices" and more particularly, "you only have i and j left". I have tried working backwards, and it seems like the terms "m" and "n" need to be something particular for these equations to hold. I am able to expand the equation into a matrix format, however I would like to understand the concepts behind it, because at the moment I am simply just working backwards

Thanks, Nick

 

[davidmoore63@y]

I was suggesting that perhaps [C] = Sigma (m=1 to 3) Sigma (n=1 to 3) of C(i,j,m,n)