- #1
barboza.g
- 3
- 0
Hi people,
In my college laboratory we were assigned an experiment to measure the hysteresis curves of a certain ferromagnetic material at different temperatures. Sounds simple, right? Well, the block of Monel 400 we chose did something weird.
We cooled it down to about -200°C and set about to measuring its spontaneous magnetism as it heated up (read below for experimental setup). We were expecting it to approach zero at a Curie temperature of 10°C and adjust our measured values using the function [itex]M\propto (T-T_c)^\beta[\itex]. However, the magnetization did the following:
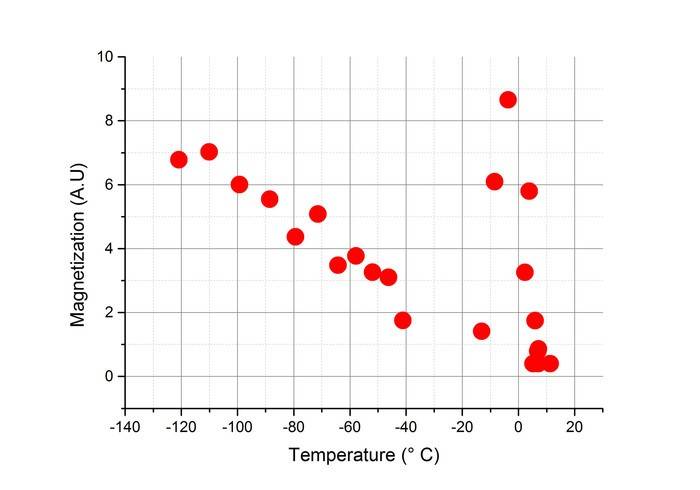
Basically, our spontaneous magnetization disappeared at about -32°C, came back with a vengance at 0°C and disappeared again at 10°C. After the material passed its Curie temperature of 10°C it behaved paramagnetically (its observed magnetization was very small); however, between 32°C and -10°C it obtained very large magnetizations, as if the hysteresis curve got really thin and then wider again.

Does anyone know why this is happening? We currently have two ideas:
Experimental setup:
We created an time-varying external field using a solenoid hooked up to an AC power supply, and measured the voltage drop over a resistance connected between the solenoid and the generator. This voltage drop is proportional to the current via Ohm's law, which is proportional to the external field considered constant over a small region in space for a given instant in time. The material subjected to the external field acquired a time-varying magnetization.
We placed two smaller solenoids connected to each other over the large one in such a way that they each canceled out any induced fields and measured the voltage drop over them (which at this point was zero). Now we placed the ferromagnetic material inside one of the small solenoids: its varying magnetic flux through it created an electromotive force. We connected the solenoids to an op-amp integrator circuit and measured the output, which is proportional to the magnetic flux, which is proportional to the induced magnetization.
Then we graphed the magnetization as a function of the external field, and took the values of the spontaneous magnetization as being proportional to the flux when there was no current across the primary solenoid.

P is the primary solenoid, B1 and B2 the two smaller solenoids.
In my college laboratory we were assigned an experiment to measure the hysteresis curves of a certain ferromagnetic material at different temperatures. Sounds simple, right? Well, the block of Monel 400 we chose did something weird.
We cooled it down to about -200°C and set about to measuring its spontaneous magnetism as it heated up (read below for experimental setup). We were expecting it to approach zero at a Curie temperature of 10°C and adjust our measured values using the function [itex]M\propto (T-T_c)^\beta[\itex]. However, the magnetization did the following:
Basically, our spontaneous magnetization disappeared at about -32°C, came back with a vengance at 0°C and disappeared again at 10°C. After the material passed its Curie temperature of 10°C it behaved paramagnetically (its observed magnetization was very small); however, between 32°C and -10°C it obtained very large magnetizations, as if the hysteresis curve got really thin and then wider again.
Does anyone know why this is happening? We currently have two ideas:
- At a certain point, our bar of Monel 400 got covered in ice. Since the area contained by the curve is proportional to the heat dissipated by the material, maybe the fact that it was covered in ice isolated it from the room and forced the hysteresis curve to become very thin.
- It's not actually Monel 400 (very possible, nobody in the lab really knows what the bar is made of) and rather a more exotic material with antiferromagnetic behavior in a certain temperature range. (This is what our lab professors think might be happening).
Experimental setup:
We created an time-varying external field using a solenoid hooked up to an AC power supply, and measured the voltage drop over a resistance connected between the solenoid and the generator. This voltage drop is proportional to the current via Ohm's law, which is proportional to the external field considered constant over a small region in space for a given instant in time. The material subjected to the external field acquired a time-varying magnetization.
We placed two smaller solenoids connected to each other over the large one in such a way that they each canceled out any induced fields and measured the voltage drop over them (which at this point was zero). Now we placed the ferromagnetic material inside one of the small solenoids: its varying magnetic flux through it created an electromotive force. We connected the solenoids to an op-amp integrator circuit and measured the output, which is proportional to the magnetic flux, which is proportional to the induced magnetization.
Then we graphed the magnetization as a function of the external field, and took the values of the spontaneous magnetization as being proportional to the flux when there was no current across the primary solenoid.
P is the primary solenoid, B1 and B2 the two smaller solenoids.
