Label propagation equation: what are the terms?

[Master1022]

TL;DR Summary

What terms in the equation (from the linked paper) are vectors or scalars?

Hi,

This is a simple question that I just wanted to clarify. I was reading the following paper on label propagation: HERE and I can't understand whether the terms are vectors or scalars in one of the equations - specifically, equation (2.15) shown in the image below.

My understanding:
- $f$ is a vector
- $S$ is a matrix
- $\alpha$ is a scalar
- I am not too sure about $y$: could be a vector or a scalar.
- $\nu$: I am not too sure, but I think it could be referring to a specific node? That is, $f(\nu)$ could be the value of the vector $f$ at node $\nu$.
- $y$: I am not sure, but I think it is a vector (see reasoning below).

Case is $y$ is a scalar:
- That would make sense mathematically, but does that mean that we are using the same scalar $y$ the equation for all nodes. That is, it doesn't matter what node $\nu$ we are considering, we will always have the same $y$ scalar in the equation? However, there is another equation above (shown below) which uses y as follows. This suggests that $y$ is a vector because then we have matrix-vector multiplication:

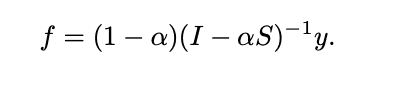
Case if $y$ is a vector:
- It could be a vector (as suggested by image above), but then we are adding a vector $(1 - \alpha) y$ to a scalar $\alpha S f$ is a vector, and we are extracted the value at a certain node $\nu$, so it is a scalar. Therefore, it seems unlikely that $y$ is a vector unless my interpretation of $\nu$ is incorrect.


Apologies if this is sparse with information. I didn't want to rewrite the paper in this post and I am unsure of some of the definitions of variables in there. Any help would be greatly appreciated.

 

[DrClaude]

$f$ and $y$ are functions of $v$, where $v$ designates a vertex, $S$ an operator, $\alpha$ a positive scalar.

For a given set of vertices $V$, it is possible to write $f$ and $y$ as a vector over the set of vertices, and $S$ as a matrix.

Note that $y$ can't be a scalar otherwise eq. (2.15) would represent the sum of disparate elements.

 

[Master1022]

$f$ and $y$ are functions of $v$, where $v$ designates a vertex, $S$ an operator, $\alpha$ a positive scalar.

For a given set of vertices $V$, it is possible to write $f$ and $y$ as a vector over the set of vertices, and $S$ as a matrix.

Note that $y$ can't be a scalar otherwise eq. (2.15) would represent the sum of disparate elements.

Many thanks for the response!

So would $f( \nu )$ be a vector instead of just referring to the entry of vector $f$ corresponding to $\nu$?

 

[DrClaude]

So would $f( \nu )$ be a vector instead of just referring to the entry of vector $f$ corresponding to $\nu$?

I don't understand your question.

$f(v)$ is a function, but if you have a discrete set $V$ of vertices $v$, then $f(v)$ over $V$ can be written as a vector.