Lachlan's question via email about the Bisection Method

[Prove It]

Perform four iterations of the Bisection Method to find an approximate solution to the equation

$\displaystyle 11\cos{ \left( x \right) } = 1 - 2\,\mathrm{e}^{-x/10} $

when it is known there is a solution in the interval $\displaystyle x \in \left[ 4.65, 4.82 \right] $

The Bisection Method solves equations of the form $\displaystyle f\left( x \right) = 0 $ so we must write the equation as $\displaystyle 11\cos{ \left( x \right) } - 1 + 2\,\mathrm{e}^{-x/10} = 0 $. We can then see that $\displaystyle f\left( x \right) = 11\cos{ \left( x \right) } - 1 + 2\,\mathrm{e}^{-x/10} $.

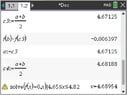
I have used my CAS to solve this problem.

View attachment 9654

View attachment 9655

View attachment 9656

After four iterations, we accept $\displaystyle c_4 = 4.68188 $ as the root.

I also told the CAS to solve the equation, and this solution is correct to two decimal places, which is very reasonable considering how slowly the Bisection Method converges.