Lagrangian Dynamics - Grandfather Clock?

[jabgaunt92]

Homework Statement

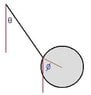
The pendulum of a grandfather clock consists of a thin rod of length L (and negligible mass) attached at its upper end to a fixed point, and attached at its lower end to a point on the edge of a uniform disk of radius R, mass M, and negligible thickness. The disk is free to rotate about the point of attachment. Assume all motion is constrained to a single vertical plane near the Earth's surface. Neglect friction and air resistance, as well as the rotation of the earth.
What is the Lagrangian for this system?

Homework Equations

L=T-U

The Attempt at a Solution

My difficulty arises in the kinetic energy term. Could someone try and show me some sort of method to finding this? Thanks

 

[TSny]

Hello, jabgaunt92. Welcome to PF!

Take a stab at constructing the kinetic energy so we can see where your difficulty lies. Note that the kinetic energy is purely rotational.

 

[jabgaunt92]

Well, I am sure that this system is analogous to a double pendulum. So I will use the generalised co-ordinates θ,∅. θ: angle the rod makes with the attached point on the disk. ∅:angle the disk makes from the attached point to its COM. Now, I do not think we use
T=1/2 M v^2 as this does not involve a moment of inertia term. I think that somehow we must use T=1/2 I ψ^2 where ψ is some combination of the two angles. Now, as I know it is a double pendulum and I also know what the Lagrangian should be if the disk was fixed I made a guess at T=1/2 I (θ(dot)^2 + ∅(dot)^2 - θ(dot)∅(dot)cos(θ-∅)).

 

[TSny]

OK, so the disk is free to pivot about the point where it is attached to the rod. Just to make sure of how you are defining $\theta$ and $\phi$, are you measuring each of the angles from the vertical, as in the attached figure?

You may write the KE of the disk as the sum of the kinetic energy due to the motion of its center of mass plus the kinetic energy due to rotation about the center of mass:

$T = \frac{1}{2} M V_c^2 + \frac{1}{2} I_c \omega ^2$

You are going to need an expression for $V_c$ in terms of the two angles. First construct expressions for the x and y coordinates of the center of the disk in terms of the angles. Then you can differentiate them with respect to time to get the x and y components of the velocity of the center of mass.

 

[jabgaunt92]

This is what I originally did and got:

V^2= L^2 ∅(dot)^2 +R^2 θ(dot)^2 +2LR∅(dot)θ(dot)cos(∅-θ)

However, I was doubtful to this as when ∅=θ should the result not reduce to 1/2 I ∅(dot)^2?

Also, is the moment of inertia about the COM or at the point at which it is pivoted?

Thanks

 

[TSny]

This is what I originally did and got:

V^2= L^2 ∅(dot)^2 +R^2 θ(dot)^2 +2LR∅(dot)θ(dot)cos(∅-θ)

Good. Although it appears to me that you have switched $\theta$ and $\phi$. I thought $\theta$ was defined as the angle the rod makes to the vertical. Otherwise, I think you have the correct expression.

However, I was doubtful to this as when ∅=θ should the result not reduce to 1/2 I ∅(dot)^2?

Everything will reduce to the correct expression for the case $\phi = \theta$ once you also include the KE of rotation about the COM.

Also, is the moment of inertia about the COM or at the point at which it is pivoted?

In the expression $\frac{1}{2}I_c \omega ^2$, $I_c$ is the moment of inertia about the COM.

For the special case where $\phi$ always equals $\theta$ you should find that the total KE reduces to the form $\frac{1}{2}I_p \dot \theta^2$ where $I_p$ is the moment of inertia about the point $p$ at the fixed end of the rod.

 

[jabgaunt92]

Yes I originally reversed the angles as you said. This has cleared up my problem now. Thank you for the help.